その他の研究事例


非線形力学系理論に基づいた金融工学
(Nonlinear Financial Engineering)

　東日本大震災やリーマンショックなど，自然や経済システムは予期せぬ振舞いによって我々を翻弄させます． 本プロジェクトは，より安心な暮らしを実現するために既存の時系列解析・予測手法を根本的に見直します． 特にこれまで軽視されてきた要素として，現象を生み出す背景ダイナミクスの存在に着眼し， この諸特性(決定論性・非線形性・非定常性・構造変化)を破壊しないデータの観測手法から再検討します． さらに，決定論性や非線形性に基づく高次の予測モデルを用いて予測精度向上を目指すアプローチの他に，予測困難な部分はリスクとして譲歩しつつも， この予測リスクを事前に推定し，統計的技法を駆使してこの予測リスク自体を緩和させるアプローチを検討します． この2つのアプローチを両輪として，信頼性に優れた時系列解析技法を確立すると共に，金融工学への応用事例として新しい非線形金融工学(NFE)を検討します．


図1: 本NFEプロジェクトは，(1)データの観測，(2)解析，(3)応用の3部門から成り，新しい時系列解析技法の確立とその応用を目指す一連の学術的体系を構成します.




(1)【観測】決定論的ジャンプ過程のサンプリング手法の再考

　自然災害や経済危機はニューロンの発火のように突然起こります． 地震や株価変動は，離散的に不等時間間隔で変動する自然現象であり，これをジャンプ過程と呼びます(図2)． しかし闇雲に突然システムがジャンプするとは考えられず， ニューロンの活動電位のようにシステム内部に存在する背景活動に起因して現象が生み出されていると考えられられます． このようなジャンプ過程を，我々は「決定論的ジャンプ過程」と呼んでいます．

　同様に金融市場でも価格変化は不等時間間隔でジャンプするものの， 価格変化を生み出すディーラー達の思惑や国際情勢は絶えず連続的に変化しています． このような決定論的ジャンプ過程を観測する方法は，2通り考えられます(図2の表)． 背景活動の物理時間に従うには，ジャンプ過程x(t)を等時間間隔Sでサンプリングすれば良いですが， このSを最適化しないと欠損や重複の発生によってジャンプ波形が破壊されてしまいます． これを防ぐためには，ジャンプ生起時刻t_n毎でサンプリングすれば良いですが， しかし背景活動の物理時間を完全に無視することになり，背景活動のダイナミクスは破壊されてしまいます． さらに多変量解析においては，各変量間の時刻が揃わないため根本的に解析不可能です． そこで我々の先行研究( T.Suzuki,PRE,2011 )では，これらの観測手法のジレンマを指摘しPhysical Review Eに掲載されました． さらに，株価変動をブラウン運動と結論づけてきた過去の多くの研究は，単に解析に用いた時間スケールの誤りである可能性を指摘し， 等時間サンプリング間隔Sを最適化する重要性を述べております．

　これまでの研究によって，単変量データに対する大まかな結論は得られております．これからは多変量解析に着手します． 前述のとおりジャンプ生起時刻t_nのサンプリングでは， 各変量のサンプリング時刻を揃えられないといった根本的な問題が生じます． そこで等時間間隔のサンプリングを導入し，重複や欠損を最小にするようにアルゴリズムで観測タイミングを最適化する手法を考案します． さらに現実のシステムを考慮すると，システムの構造が非定常的に変化している可能性があります． 次の(2)[解析]の工程では，異質な学習データが混合すると解析能力低下の原因となりますので， システムの構造変化を検知しながらデータをサンプリングする必要があります．

　データのサンプリングは，システムを分析するうえで最も重要なプロセスであります． データ内に有用な情報が欠落すれば，いかに優れたデータ解析手法を駆使しても無力となるからです． また，サンプリング方法を見直すことはシステムを記述する時間を定義することでありますので，物理学の観点からも大変重要な問題です．

[参考文献]
■ T. Suzuki: "Appropriate Time Scales for Nonlinear Analyses of Deterministic Jump Systems,"　Physical Review E, Vol.83, No.6, 066203, 2011.
■ 大塚陽介，鈴木智也:　"決定論的ジャンプ過程のシステム同定と長期予測に適したサンプリング手法の検討,"
情報処理学会論文誌 TOM, Vol.5, No.1, pp.30-39, 2012.
■ Y. Otsuka and T. Suzuki: "Data Sampling Strategies for Long-Term Predictions of Deterministic Jump Systems," Proc. of NCSP, pp.88-91, 2012.




(2)【解析】予測リスクをヘッジした「慎重な」非線形時系列解析・予測

　フーリエ解析など線形的な時系列解析手法の多くは，データの定常性を前提としています． しかし自然界のシステムの多くは動的に構造変化する非定常システムであるため， データ解析を行う際には短期の少数データに限定せざるを得ない場合があります． データ数が少なければ当然ながら解析性能は低下します． 特に時系列予測は意思決定など実用志向が強いツールであるため，予測精度の低下は深刻なダメージを及ぼす危険性があります． そこで我々の先行研究(K.Nakata,NOLTA,2012)では， 集団学習法の一種であるバギングを活用し，将来変動を確率分布で示す予測法を提案しています．

　しかし当然ながら，少数データという情報不足をカバーできるのには限界があります． そこでバギングで推定した予測分布の標準偏差に着目し，これを予測誤差の危険性すなわちリスクと考えます． さらにリスク推定の活用として，リスクが高い時は予測を避けるという選択が可能になりますので， 少数データにおいても安全な時系列予測を実現できる可能性があります． また正しい予測を行えるということは，システムの構造をより的確に捉えられることを意味しますので， これを非線形時系列解析に応用することで，カオス性を判定するリアプノフ指数解析や， システムのダイナミクスを同定するサロゲート検定法などの解析性能を向上できるでしょう．

　時系列解析は多数のデータを必要とするので，従来より長期データを解析するのが常識的であります． しかしシステムの動的変化を考慮すれば， 長期データほど複数の構造が混合する可能性が生じ，偽の結果を引き起こす危険性が高まります． したがって本研究のように，短期の少数データによる時系列予測・解析手法を検討することは極めて現実的なアプローチであると考えます．

[参考文献]
■ K. Nakata and T. Suzuki: "Evaluating the Risk of Nonlinear Prediction with the Bagging Algorithm," Proc. of NCSP, pp.748-791, 2012.
■ 仲田和也, 鈴木智也: "バギングによる非線形予測のリスク評価," 信学技報, NLP2011-60, vol.111, no.242, pp.1-6, 2011.
■ K. Nakata and T. Suzuki: "Avoiding Risk of Nonlinear Prediction with the Bagging Algorithm," 投稿中.




(3)【応用】予測リスクをヘッジする「非線形」金融工学

　上記(2)[解析]において，高リスクの時には解析をスキップすることでリスクを回避しますが， 共分散の性質を利用することで統計学的にリスクを緩和することもできます． その代表例として金融工学におけるポートフォリオ理論は， 上記(1)(2)の知見を工学的に応用できることを示す格好の題材であります．

　従来のポートフォリオ理論は，直近の株価変動の平均値や標準偏差によって期待リターンやリスクを推定しますので， 予測モデルとして考えると比較的単純なモデルに基づいています． 確かにリスク分散効果を数学的に記述できるなど学術的価値は充分ですが，実務においては如何でしょうか？ 本プロジェクトでは，先述(1)(2)のアイデアを既存の金融工学や金融テクニカル分析に活用します． まず生じる問題として，従来と予測モデルが異なりますのでリスクの定義を改める必要があります． そこで本研究では，先述(2)の集団学習法で得た将来値の予測分布に基づいてポートフォリオ理論やボリンジャーバンドを書換えます． また先述(1)に基づいて，データのサンプリング方法の違いによる予測精度およびリスク分散効果も検証します．

　ご存知のとおり，金融工学は期待リターンとリスクの2つのパラメータによってモデル化されています． ここで期待リターンは「予測値」，リスクは「予測誤差の可能性」とみなすことができるでしょう． そこで本プロジェクトでは，予測モデルを高度化することで第1パラメータを向上させ，集団学習法で第2パラメータを向上することで， これまでと異なる金融工学をご提案できればと考えております． さらにポートフォリオ効果によってリスクを分散することができますので 「予測精度向上と予測リスク低減を同時に実現する新種の時系列解析技法」と捉えられるかもしれません． なお，ポートフォリオ理論の根本は多変量データの非同期性を利用したリスク分散技術であるため，金融投資に限定するものではありません． 例えば，プログラム開発，経営戦略，マーケティングなど異分野においてもポートフォリオ理論が応用されています． したがって本プロジェクトは，今後様々な分野に貢献できる可能性を秘めています．


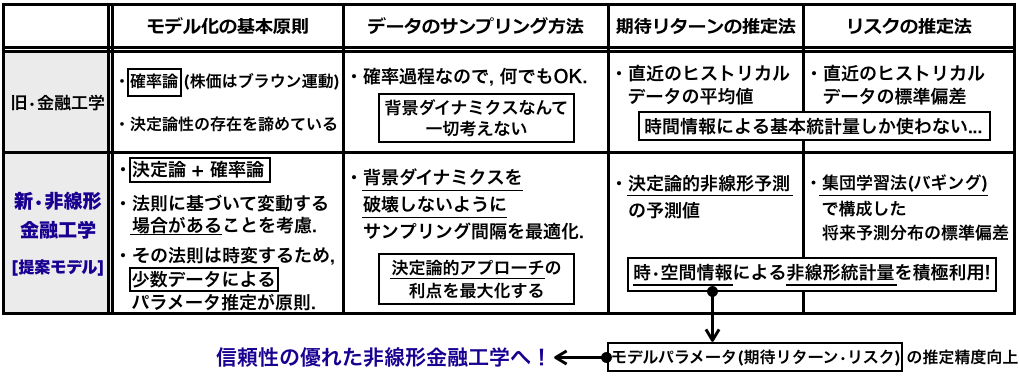
図3: 「従来の金融工学(FE)」とご提案する「非線形金融工学(NEF)」の違い.


[参考文献]
■ 鈴木智也, 猪瀬悟史, 田中清春, 林大賀, 大倉佑嗣: "金融工学における非線形時系列モデリング," IEICE総合大会講演集, AS-1-3, 2012.
■ 猪瀬悟史, 鈴木智也: "非線形時系列予測による株式ポートフォリオの運用," 信学技報, NLP2011-61, vol.111, no.242, pp.7-12, 2011.
■ S. Inose and T. Suzuki: "Stock Portfolio Management with Nonlinear Time Series Prediction," Proc. of NCSP, pp.744-747, 2012.
■ S. Inose, T. Suzuki, Kazuo Yamanaka: "Stock Portfolio Management Based on Nonlinear Prediction Model," Proc. of NOLTA, accepted, 2012.
■ T. Hayashi and T. Suzuki: "New Bollinger Bands for Nonlinear Technical Analysis of Pairs Trading," Proc. of NOLTA, accepted, 2012.
■ K. Tanaka and T. Suzuki: "Dynamical Portfolio Theory by Nonlinear Bagging Predictors," Proc. of NOLTA, accepted, 2012.
■ S. Inose, T. Suzuki, K. Yamanaka: "Tradeoff between Commission and Frequency of Rebalancing the Nonlinear Portfolio Model," Proc. of NCSP, 2013.
■ 猪瀬悟史, 鈴木智也: "ポートフォリオ構築問題における非線形時系列予測モデルの活用," 電子情報通信学会論文誌, Vol.J96-A,No.7,pp., 2013.
■ S. Inose, T. Suzuki, K. Yamanaka: "Nonlinear Portfolio Model and its Rebalance Strategy," Nonlinear Theory and Its Applications, IEICE, accepted.