複雑現象のメカニズムを探り,新しい人工物の創造に役立てる研究をしています.また,学生の向上心を実力に変えるお手伝いをしております.
|
IFTA2013: 決定論的★時空間テクニカル分析 by T.Suzuki
English version is shown here.

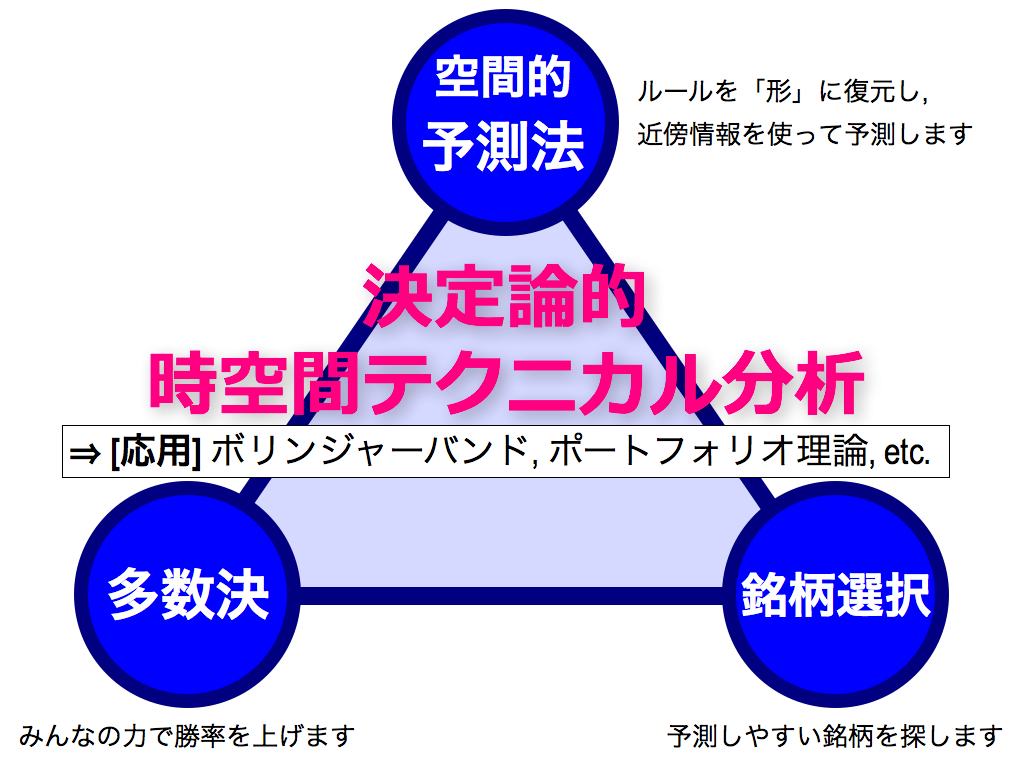
本稿は,2013年10月に開催されたIFTAサンフランシスコ大会の講演内容に基づいています. 発表に用いたスライドを日本語化して解説させて頂きます. 本稿のタイトル「決定論的時空間テクニカル分析」は,決定論的な世界観をテクニカル分析に活用した新しい市場予測法です.
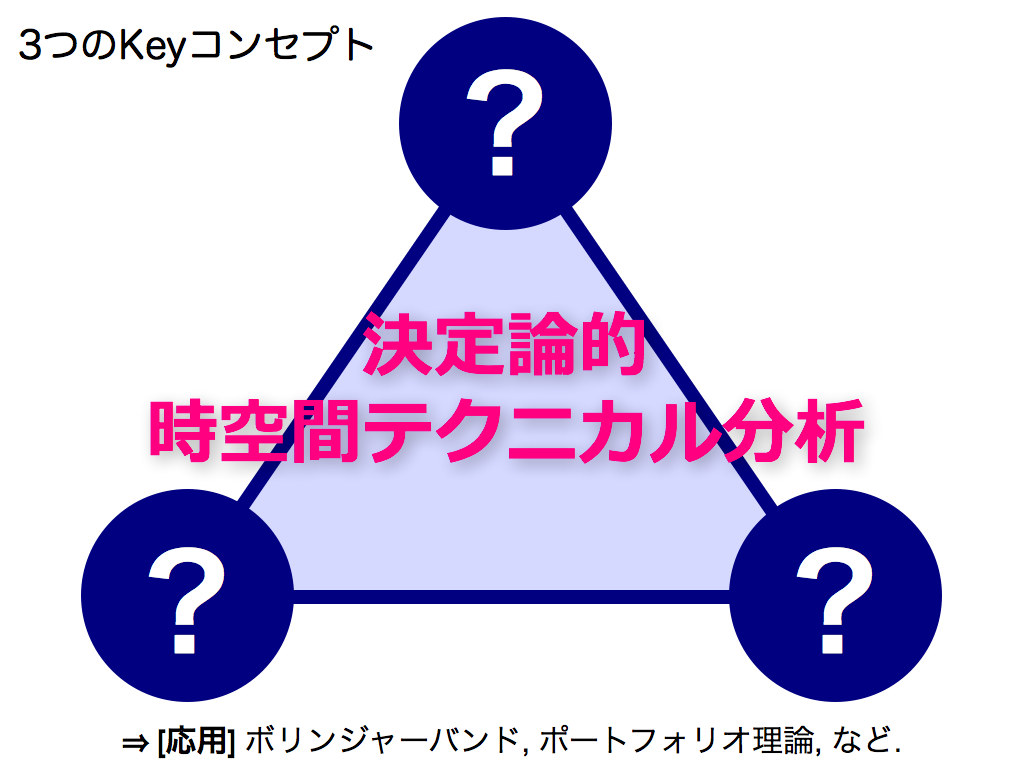
本手法のコンセプトは「3 つ」あります. 前半でこれらの詳細をご説明させて頂き, 後半で応用事例として,ボリンジャーバンドやポートフォリオ理論への適用方法を紹介させて頂きます.

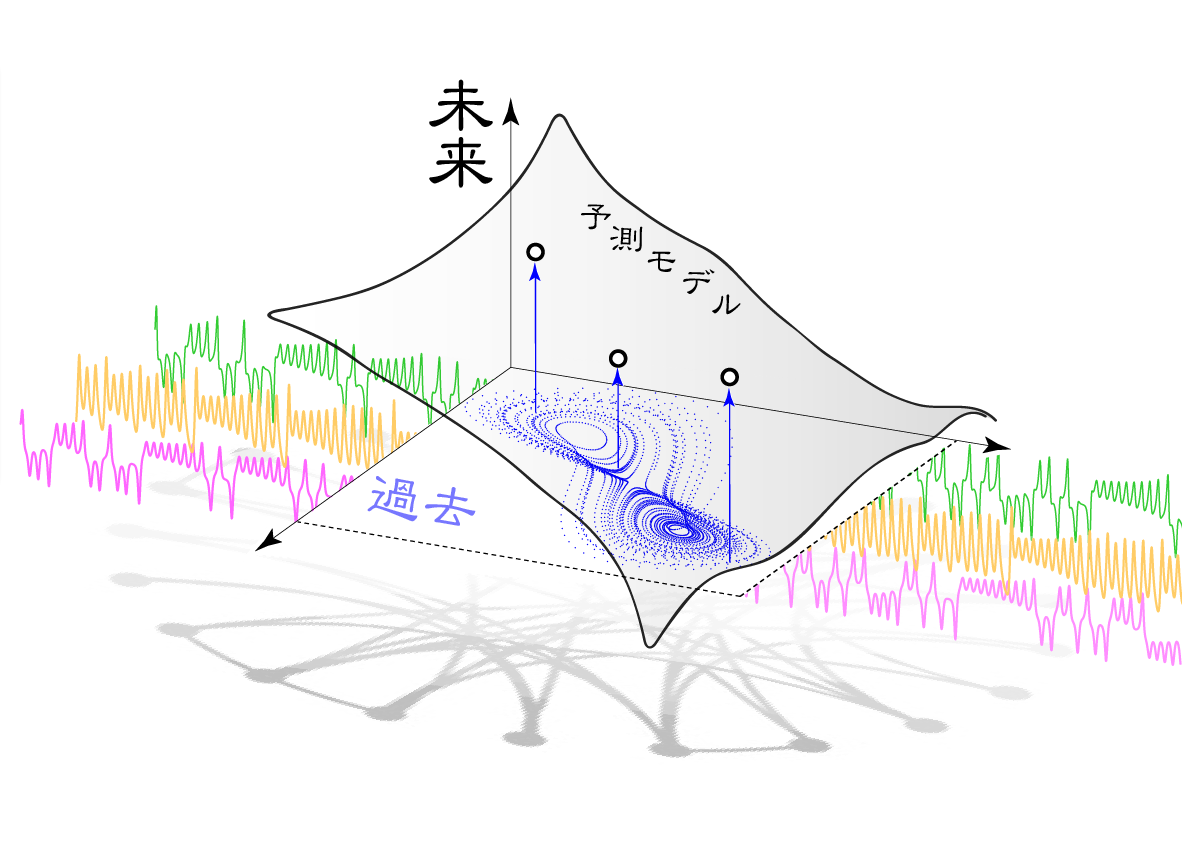
第1のカギは「空間構造の活用」です. スライド中に 「ルールF」と書いてあります. これは数学の関数 (Function)を意味し,金融市場においては,直近の株価を入力すると明日の株価を導けるようなルールFを指します. もちろんルールFが分かれば,明日を予測できます.
しかし当然ながら,このルールFは一般的に未知であり,将来予測は難しいのです. しかしここで言いたいことは,この「第1のカギ」はルールFを理解する上で大変役立つという点です. なぜなら,このルールFは空間的な模様(形)として表すことができ,我々はそれを利用することで将来予測が可能になります.
さて,これはなぜでしょう? 次のクイズを解きながら考えてみましょう.
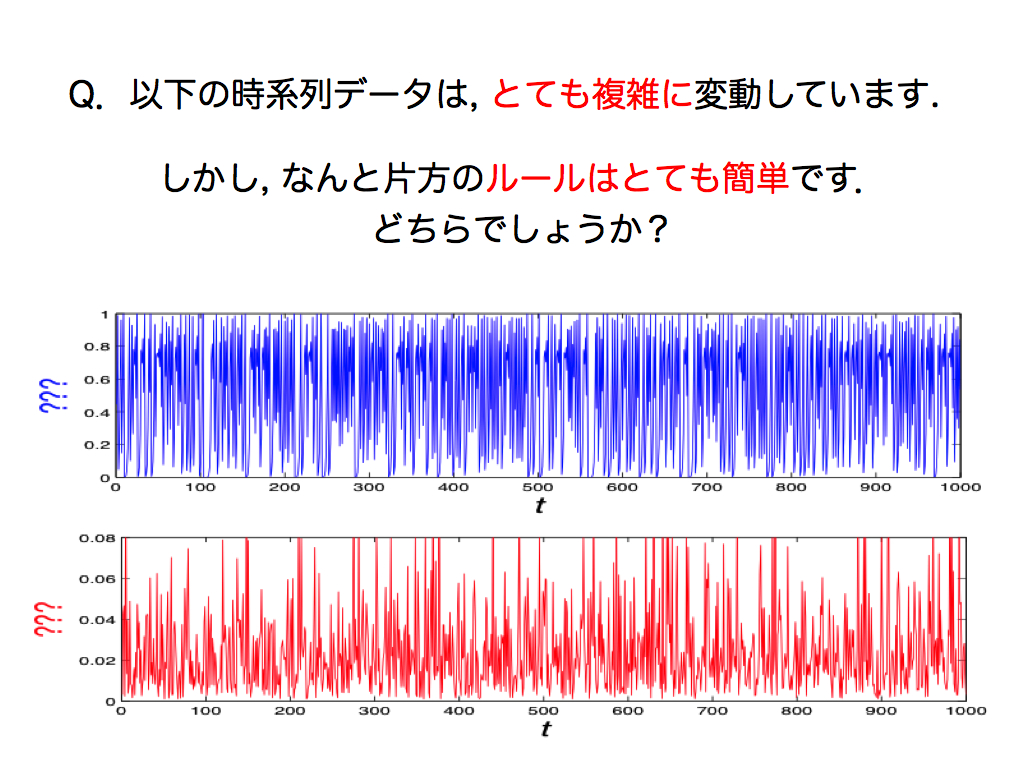
ここに2つの時系列データがあります.どちらも複雑に見えます. そこで皆さんは,これらを生み出したルール Fを理解することなんて非常に困難だと思うでしょう. しかし実は,片方のデータは非常に単純なルールによって私が作成したものです.
それはどちらでしょうか? ぜひ想像してみてください.
申し訳ございません...これは意地悪クイズです.人間の目視では解けません. でもご安心ください.これを解く良いカギがあります.そうです,先に述べた空間構造です. この時系列データ(時間表現)を「空間表現」に変換してみましょう.
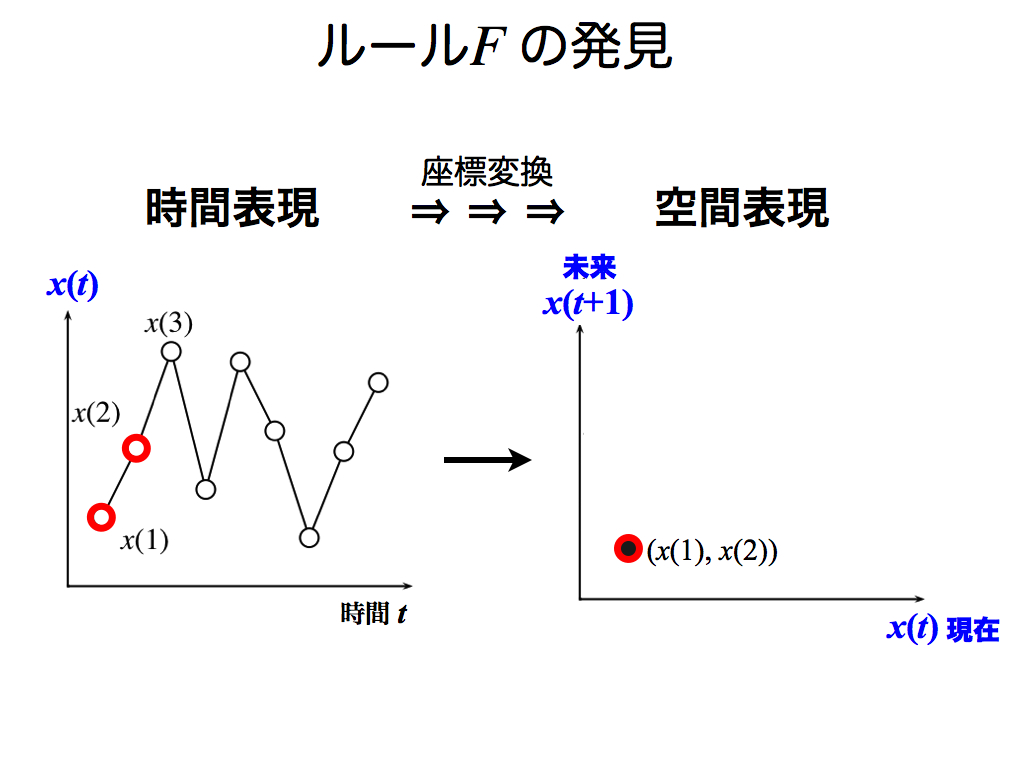
スライド中の左図は,時系列データ(時間表現)です.ここから時間が若いデータとして,x(1)とx(2)を選びます.そして,これらを右図の空間表現に変換します.
右図の横軸および縦軸は,時間tではなくデータxです.各座標間において距離を測れるので,右図を「空間」表現と称しています.一方,左図の横軸は時間tなので,時間表現です.
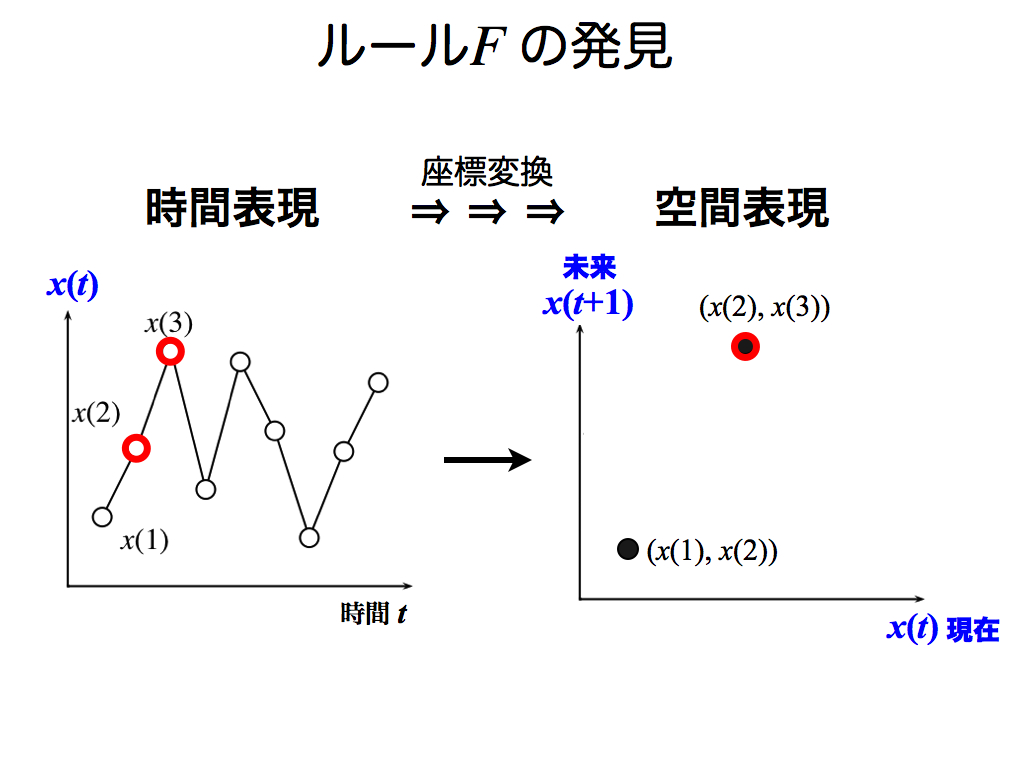
同様な変換を,時間tを進めながら繰替えします. ここではx(2)とx(3)を選び,右図に新しい点が追加されました.

同様にx(3)とx(4)を選び,右図に3点目が追加されました.
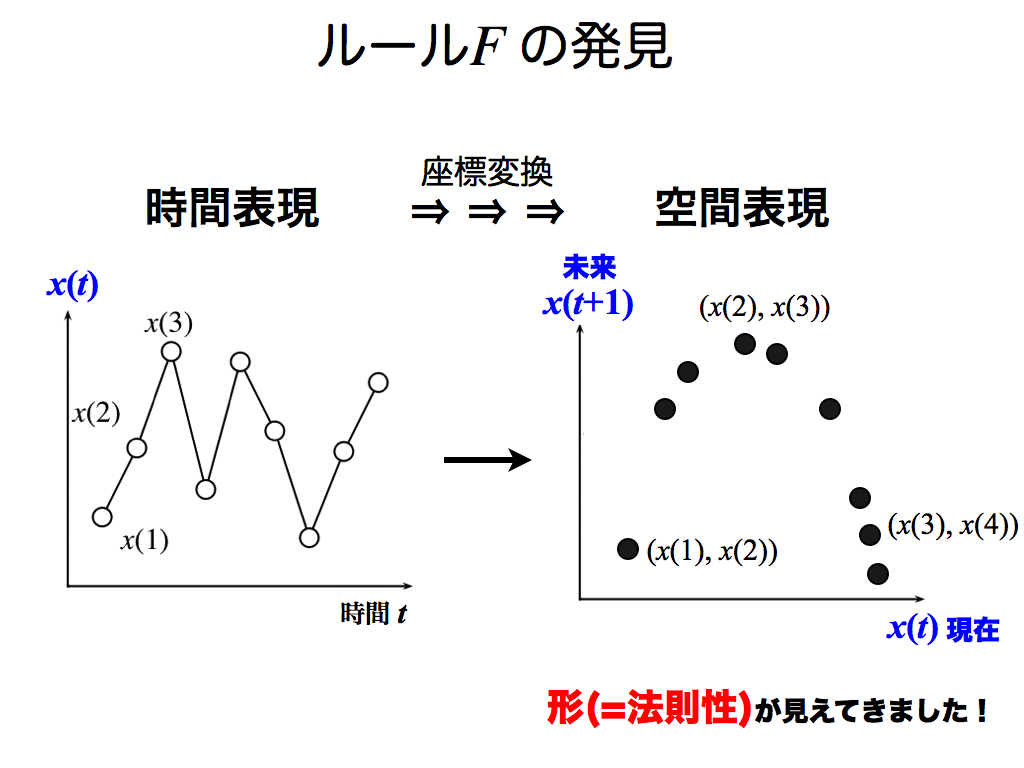
これを何度か繰返えすと…何やら形が見えてきました. 実はこれが時系列データを生み出した「ルールFの正体」です!
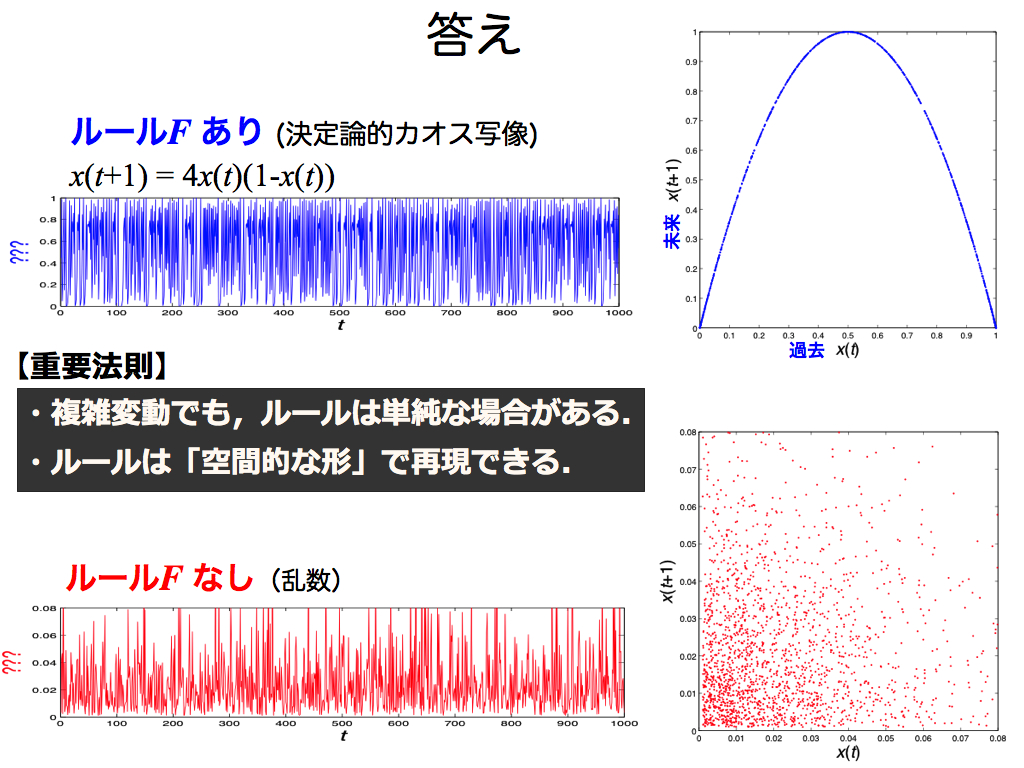
先ほどのクイズの答えです.上段の時系列データは,高々2関数のシンプルなルールFによって作成されました. 右辺には,過去データx(t)を入力として持ち,左辺のx(t+1)はルールFによって生成された出力です.つまりこの関数は,入力と出力の関係性を意味しています.
この観点より,先の空間表現も同じ意味を持ちます.横軸は過去x(t)を示し,縦軸は未来x(t+1)を示します.つまり,これも入力(過去)と出力(未来)の関係性を意味しています.だからこそ,ルールFは空間的な「形」として現れるのです.
別の根拠もご紹介しましょう.数式の右辺の括弧を外せば-x2(t)が現れます.ご存知の通り,上に凸の放物線を意味します.さて,空間表現をご覧ください.確かに上に凸の放物線になっていますよね. このように,時系列データを空間表現に変換することでルールFを知ることができ,これを利用することで将来予測が可能になるかもしれないのです.それゆえ,この「空間表現」は非常に重要なカギなのです.
一方,下段の時系列データは,乱数(ランダム)によって作成したものです.よって元々ルールFは存在しないため,空間表現に変換しても特徴的な形は出現しません.
以上により, 2つの重要な知見が得られました.一つ目は,時系列データが激しく複雑に見えても,それを生み出したルールは単純な場合があります.ですから,予測を諦めるべきではありません. 二つ目は,そのルールは「空間的な形」として再現できる点が重要です.
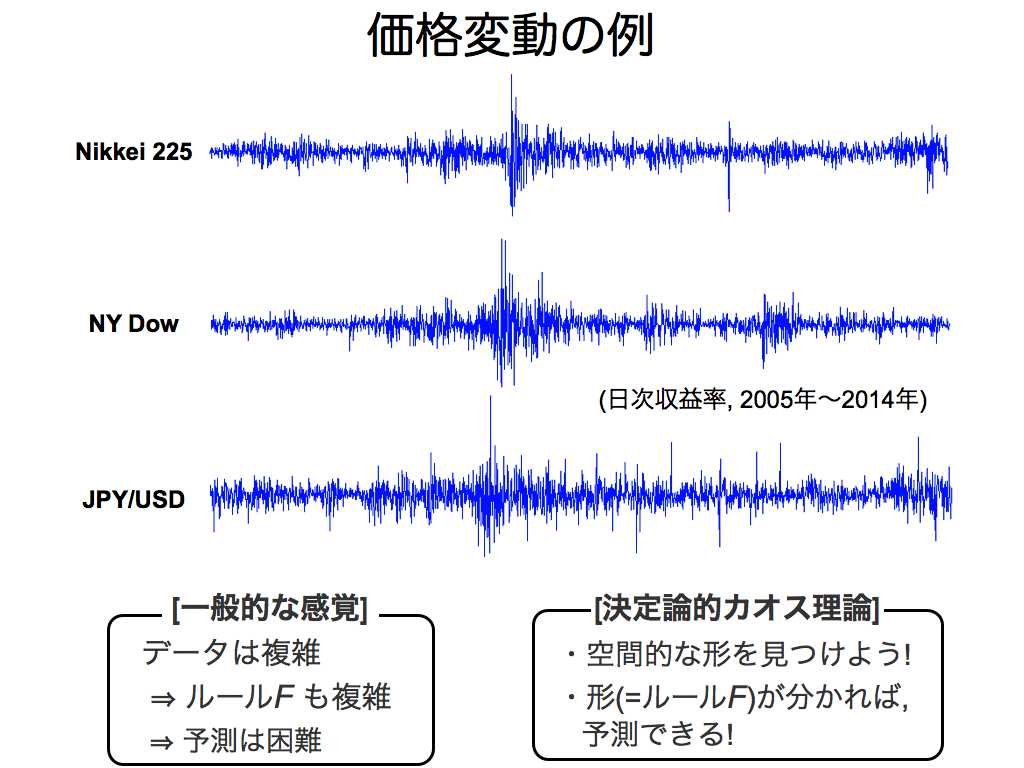
さて,実際の金融市場に適用してみましょう.これらは10年分の日次収益率の変動です.ご覧の通り,見た目は複雑です.しかし予測を諦めず,ルールFを探してみましょう.
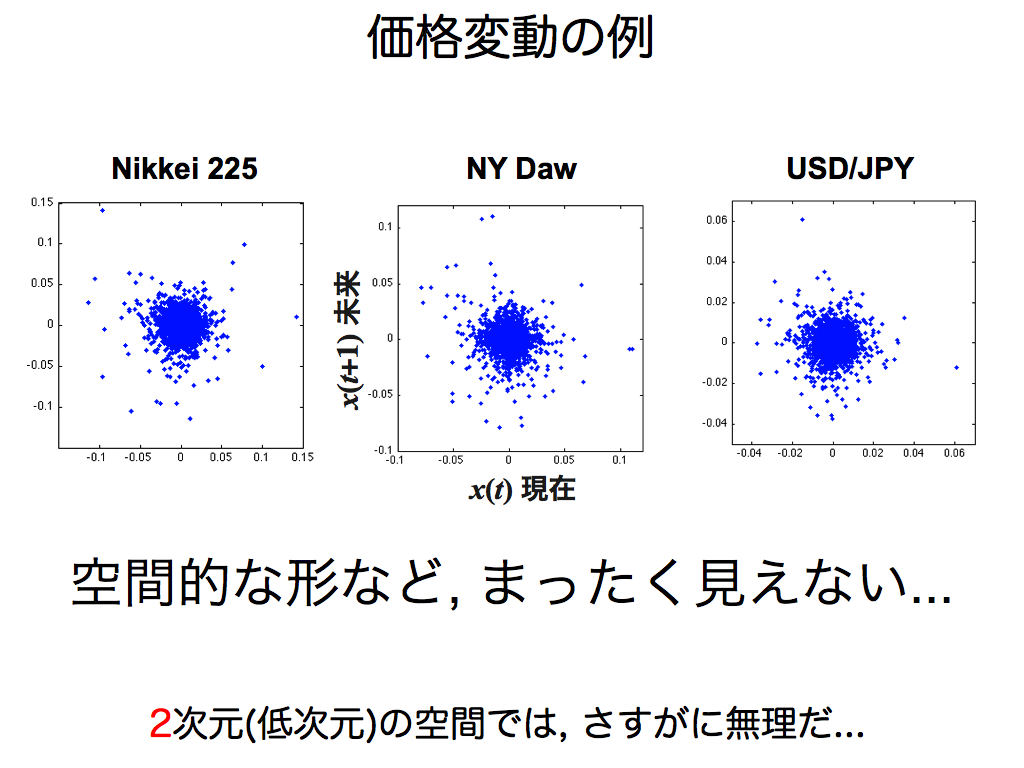
なんて事でしょうか…空間表現に変換しても,特徴的な形はまったく見えません.もしルールがあったとしても,その構造は潰されて丸められてしまったかのようです. 実は,空間の次元が低すぎる事が原因です.たとえば10次元の空間ならルールFの形を再現できるとします.しかし今回は2次元空間ですから,必然的に構造が折り畳まれて,スライドのようにぐちゃぐちゃになってしまいます.
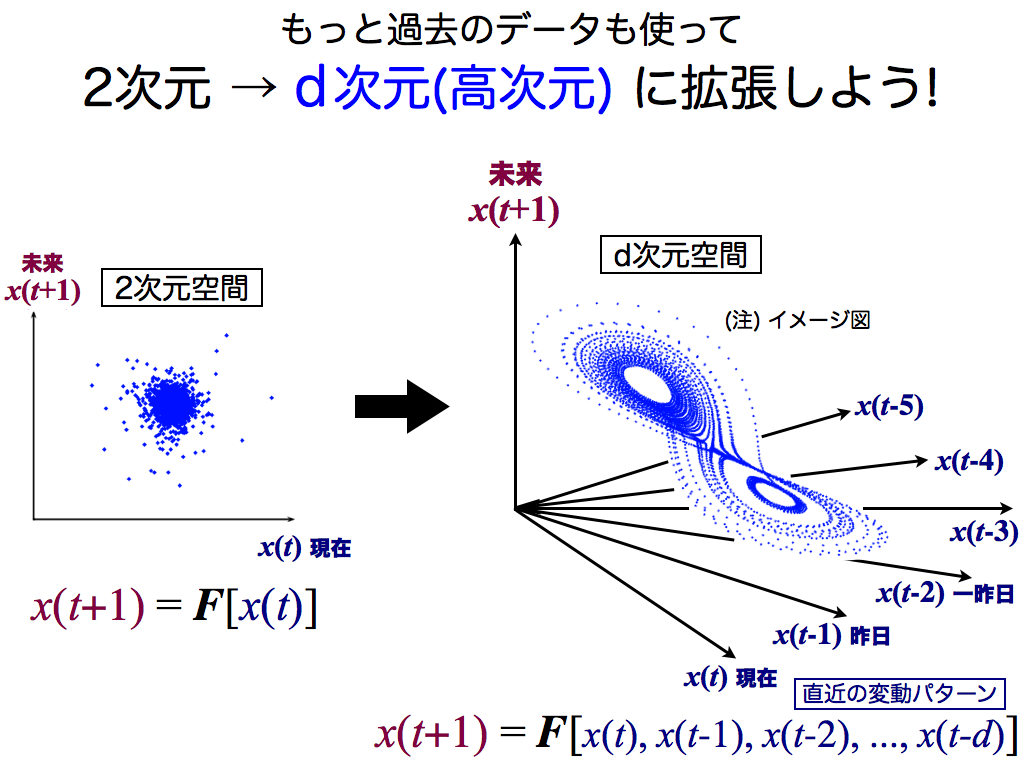
したがって,2次元以上の空間に変換するのが通常です.そのため,より多くの過去データを座標軸として用います(スライド中のx(t),x(t-1),x(t-2),x(t-3),…). これらは関数Fの入力に相当し,縦軸のx(t+1)は出力です.つまり,空間表現によって再現された模様は,入力(過去)と出力(未来)の関係性そのものであり,数式中のルールFを形で表現したものと言えます.

さて次に,この形を将来予測に利用します.スライド中の「直近」の次の動きを予測してみます.なお,これらの点は,右図の一部を拡大したものとお考えください.
幸いなことに,この予測法は極めて単純です.手順はたった2つしかありません. まず,過去のデータベースから「近傍点」(図中の黒丸)を探します.座標が近いということは,座標軸を構成する過去の変動パターンが類似していることに相当します.
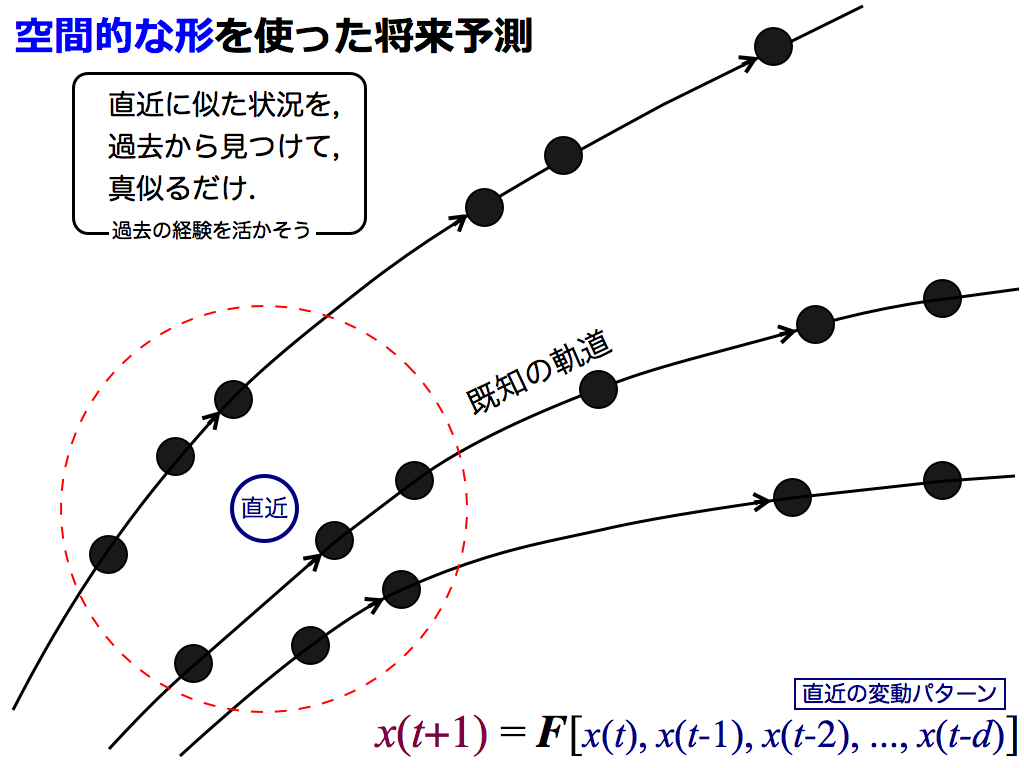
つまり関数Fへの入力が類似しているため,当然ながら,出力である将来変動も類似するはずです.
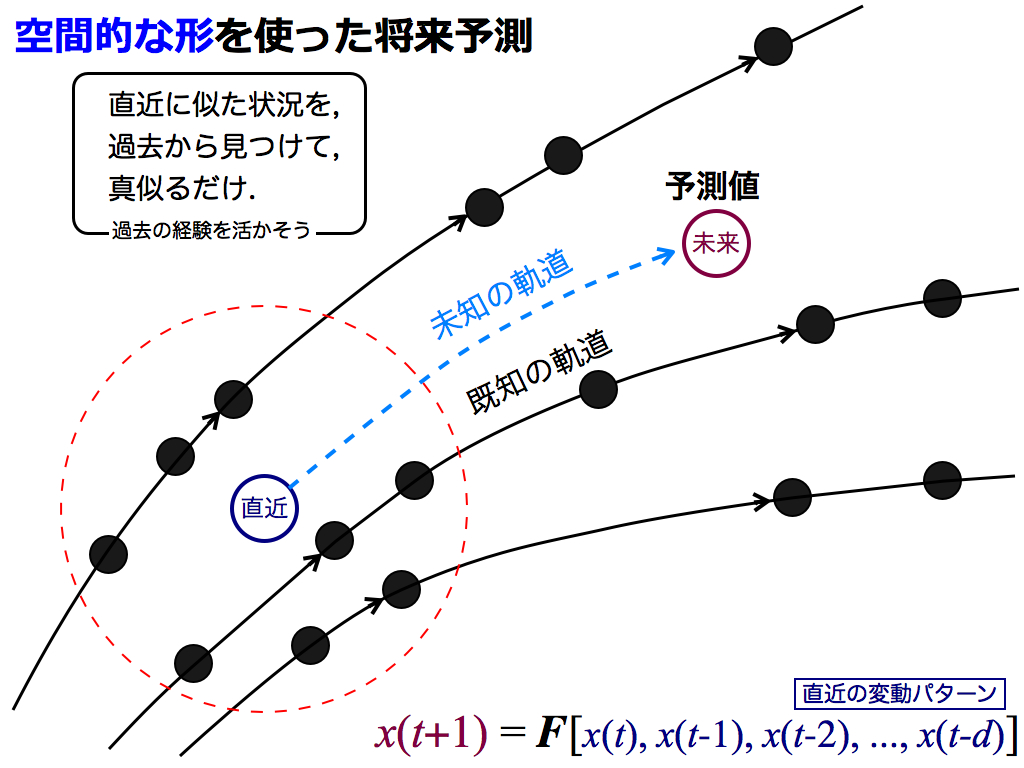
したがって第二ステップでは,近傍点の動きについて行けば良いのです.基本的にそれだけです.
実に簡単な予測法ですが,学術用語を使えば「決定論的非線形予測法」と呼ばれ,小難しく響きます.しかし単に,空間的な近傍点に着いて行くだけ,と考えて頂いて結構です.
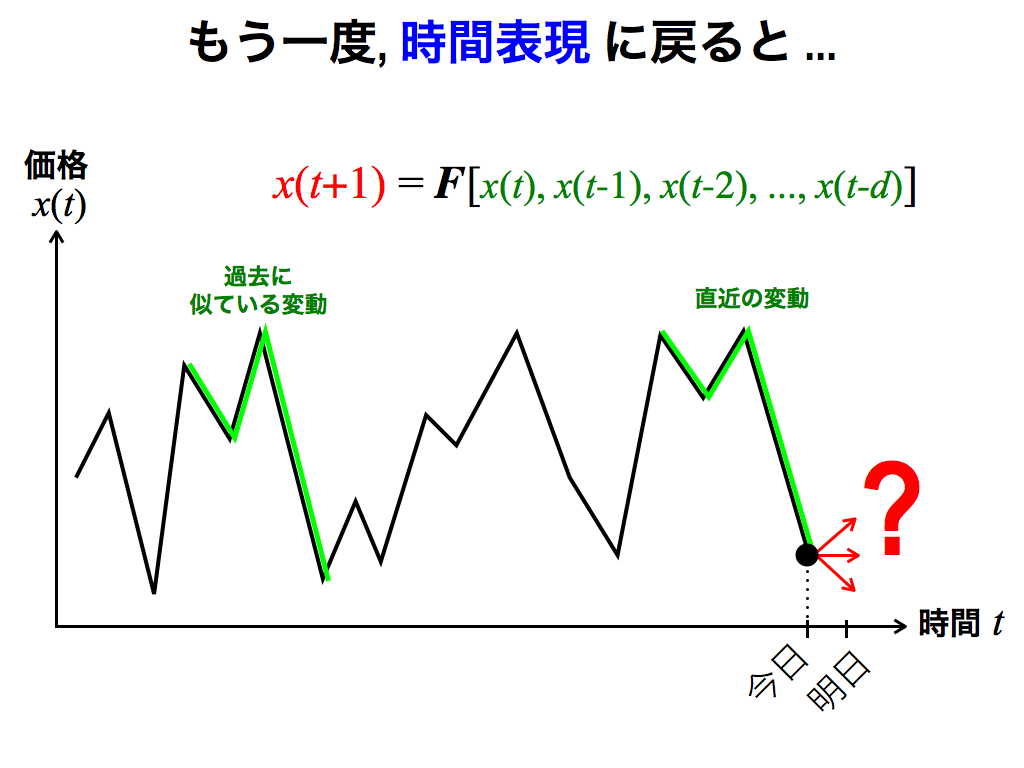
しかし空間的と称してもイメージし辛いでしょうから,馴染みのある時間表現(横軸が時間t)でも説明します.
スライドのように,明日の株価を予測したいとします. 先述の近傍点に相当するものは,直近の変動に対して「過去に似ている変動」です(図では,各変動パターンは4点で構成されているので,空間表現ならば4次元空間です). 類似した変動パターンは,関数Fへの入力が似ているわけですから,出力も類似します.
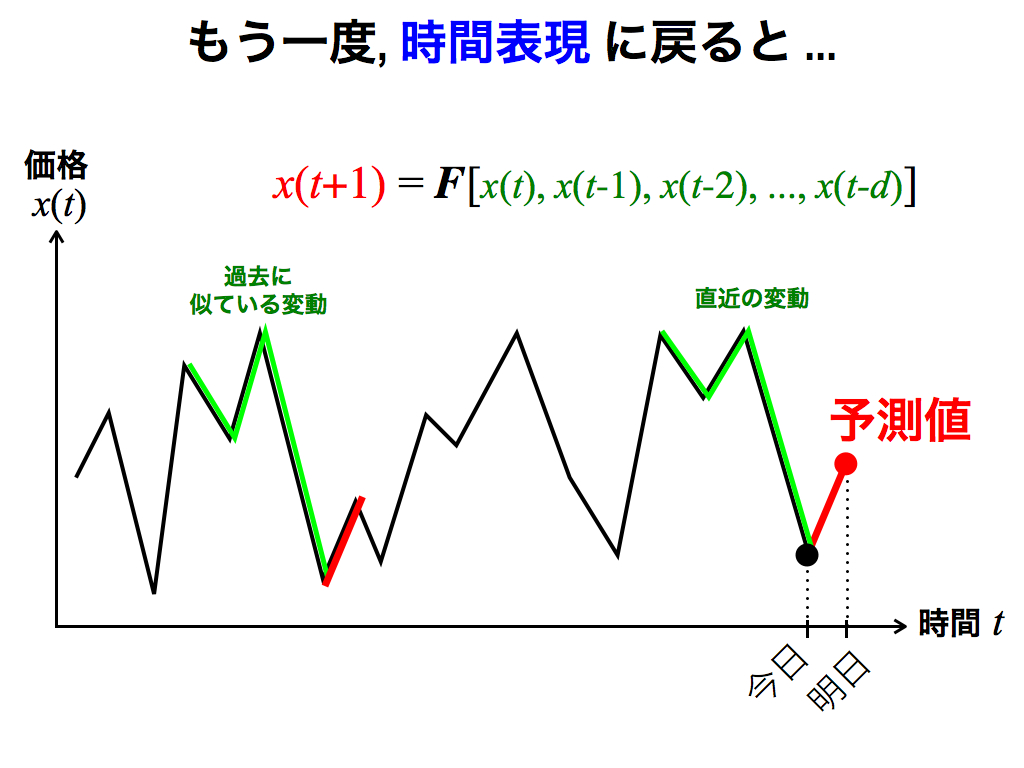
したがって予測値は,過去の類似パターンを真似すれば良いのです.

既にお気づきかもしれませんが,この決定論的非線形予測法は,テクニカル分析のフォーメーション分析とみなすこともできます.
フォーメーション分析では,典型的なフォーメーションを利用して将来予測しますが,これは先述の近傍点に相当します.つまり決定論的非線形予測法は,テクニカル分析と非常に親和的であるといえます. 「歴史はくりかえす」や「相場のことは相場に聞け」等のコンセプトは,決定論的非線形予測法にも当てはまります. しかし,役立つフォーメーションを機械的に見つける点においては,これまでのフォーメーション分析と異なります.
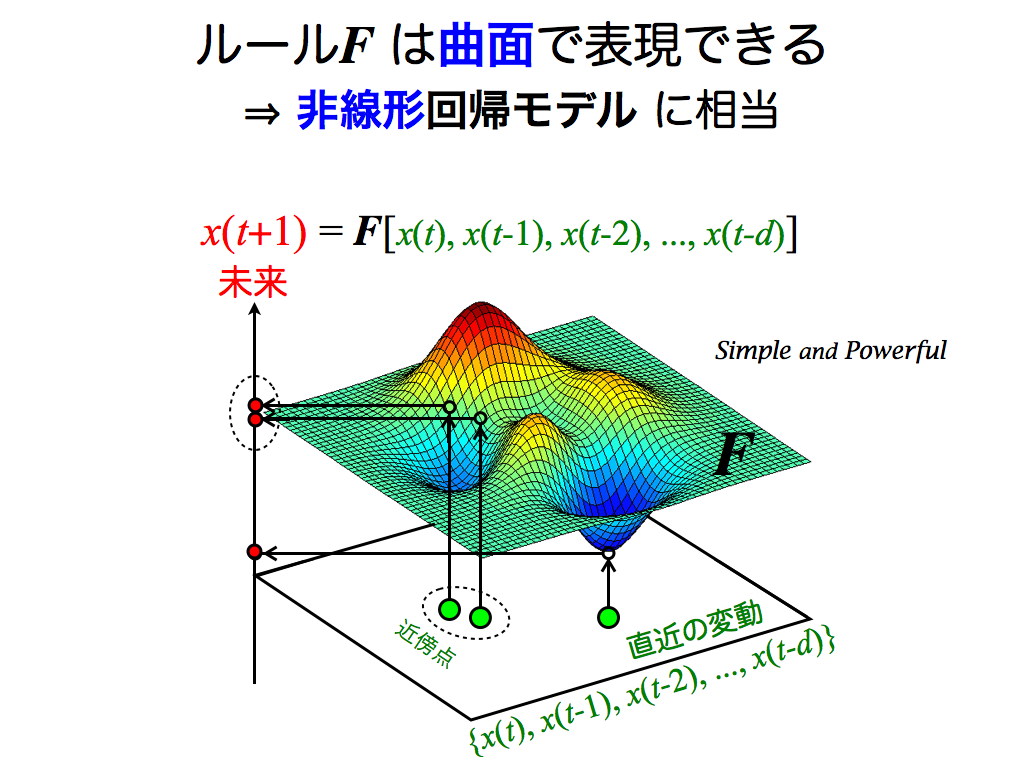
余談ですが,この予測法は「非線形モデル」に分類され,簡単ながらも非常にパワフルな予測法です. 底面の入力データ(過去)と縦軸の出力(未来)の関係性(ルールF)を,「曲面」で表現できるため「非線形」と呼ばれます. 一方,線形統計学に基づく回帰予測などは,平面(線形)でしか表現できないため,予測力において非線形(回帰)予測モデルに劣ります.
第2のカギは「多数決」です.
実は,多数決は予測精度を向上できる合理的な方法です. 理屈は簡単に証明できます.テータマイニングの分野では「集団学習」と呼ばれ,古くから利用されています. また最近流行りの「集合知(みんなの意見は案外正しい)」にも関連があります.
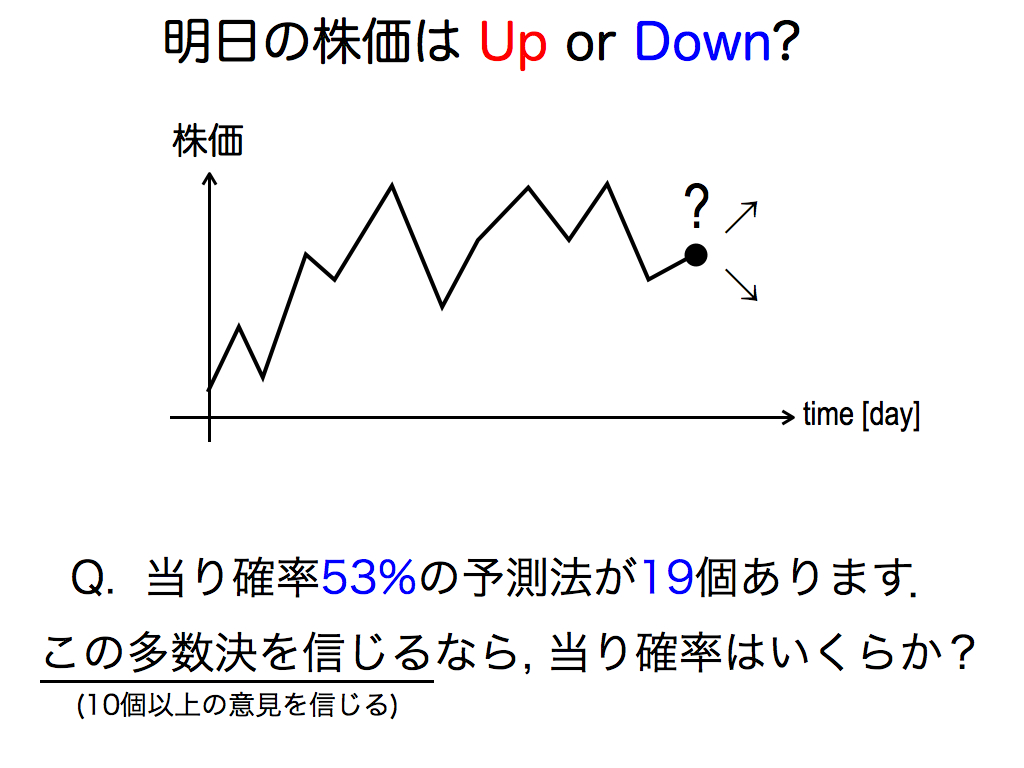
さて,再びクイズを解きながら,多数決の有用性を証明してみましょう.
明日の株価が上がるか下がるか(2択問題)を予測する際に,正答率53%の予測法が19個あるとします. この多数決を信じた場合,多数決の正答率はいくらになるでしょうか?
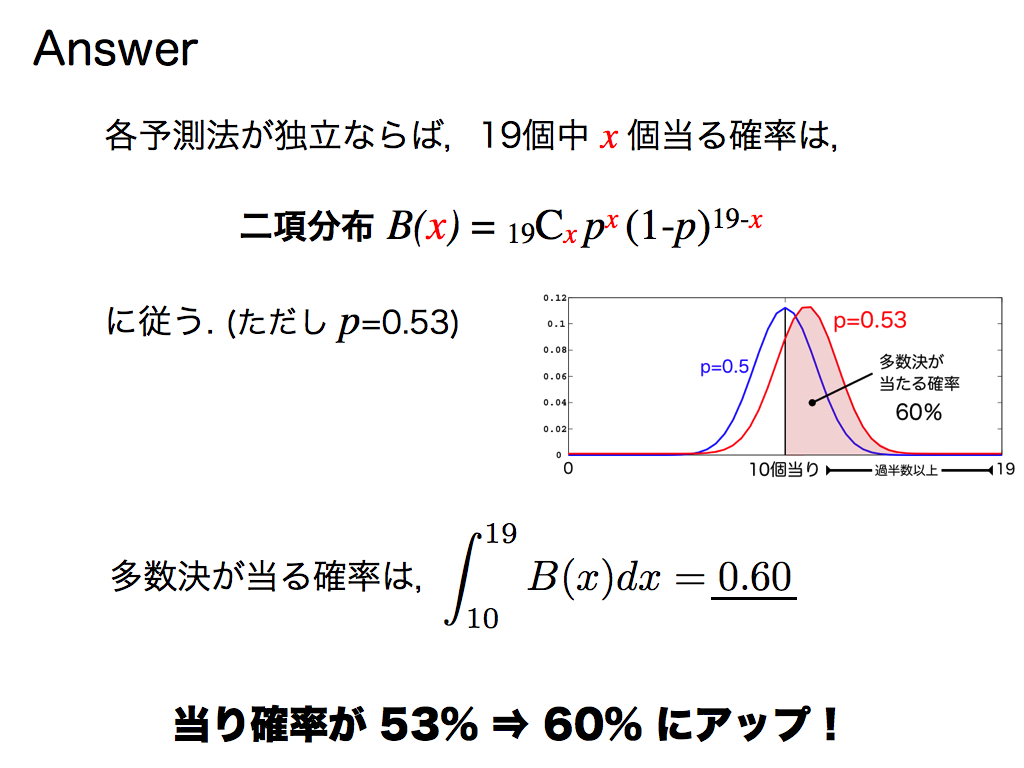
確率論の知見により,19個の予測法のうちx個正解する確率は二項分布によって記述できます.多数決とは,半数(10個)以上のコンセンサスですから,10以上のxについて二項分布を積分すれば,多数決の正答率が得られます. 結果のみをご紹介すると,なんと「0.60」になります.
これってスゴイことですよね.なぜなら,正答率53%の予測法が60%にアップしたのですから!
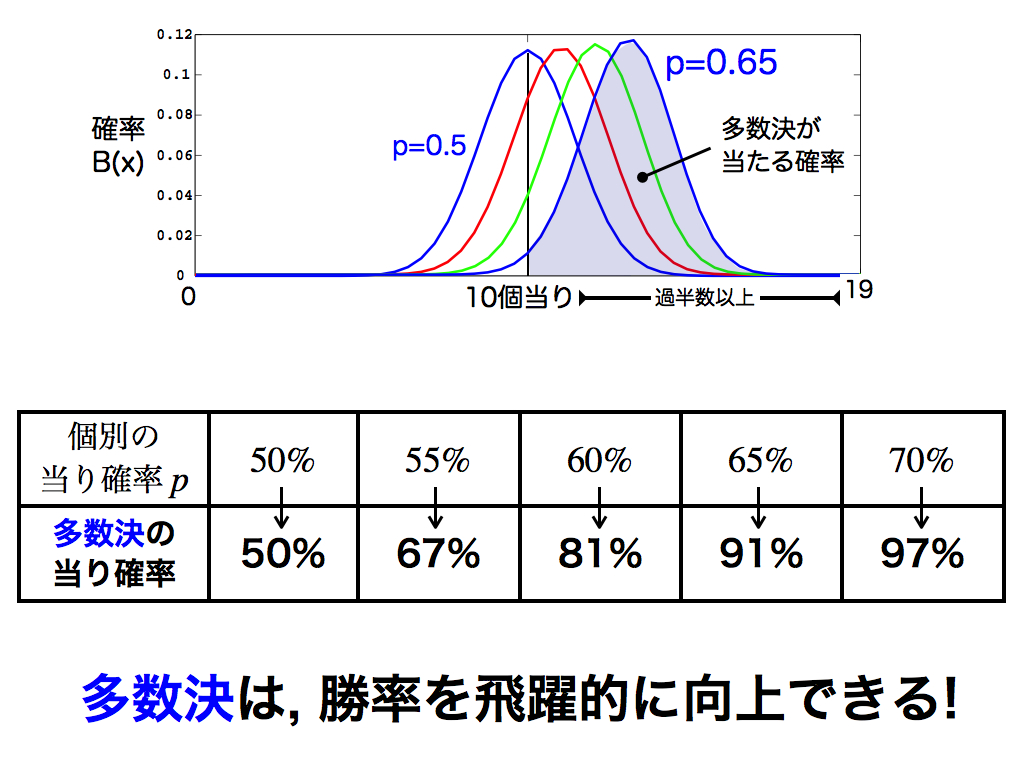
念のため,元の正答率p = 53% をいろいろ変えて多数決の効果を調べてみました.さすがに予測力が全く無いp=50%はどうにもなりませんが,p>50%において予測力の向上を確認できます.
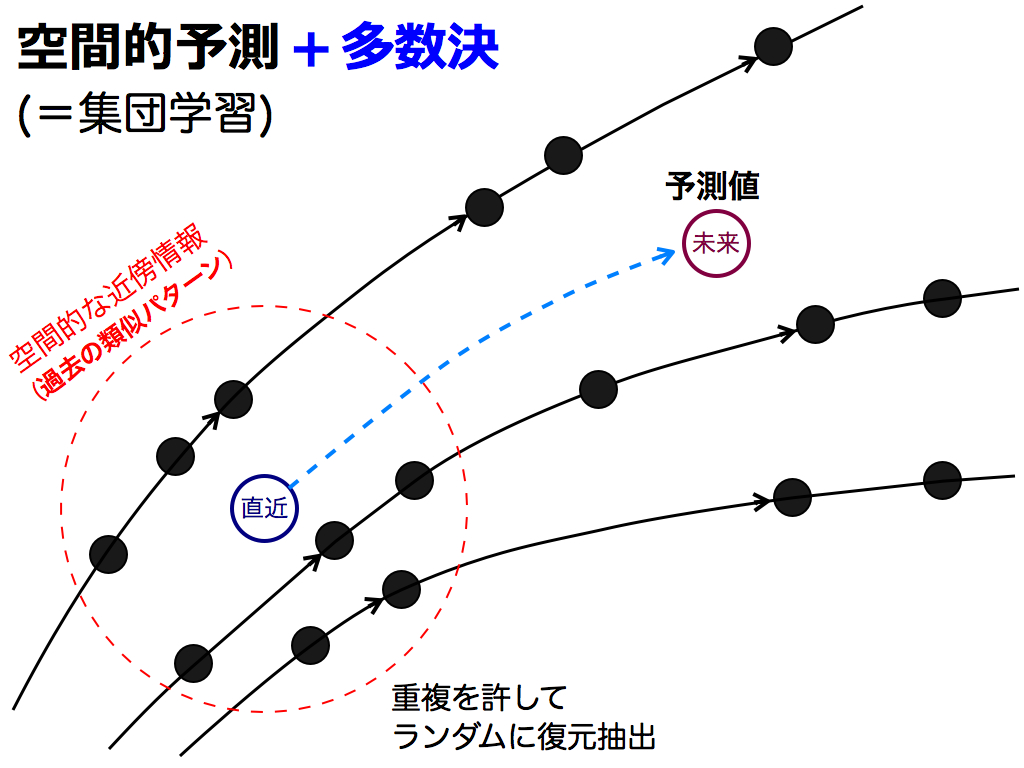
それでは,この多数決を先述の予測法に応用してみましょう.集団学習では各予測法が独立であることを想定しているので,近傍点をランダムに復元抽出して独立状態に近づけます.そして選ばれた近傍点の動きを追うことで,予測値を算出します.
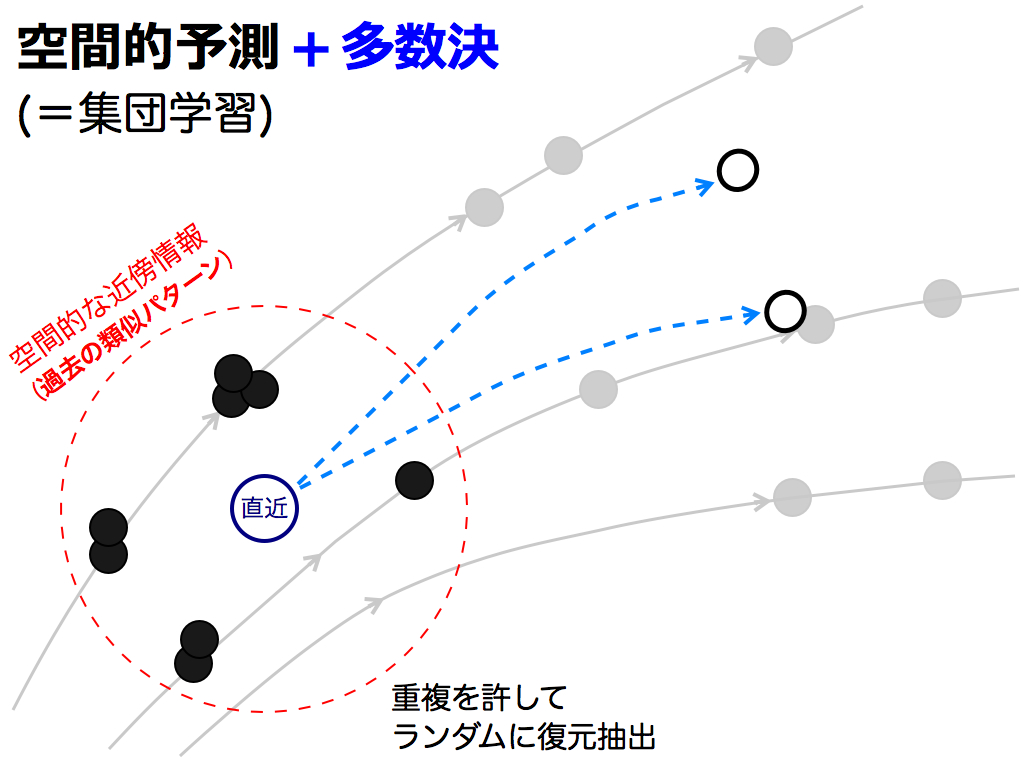
これを何度も繰返します.近傍点の抽出は,重複を許してランダムに行われるため,多様な予測値が出現します.
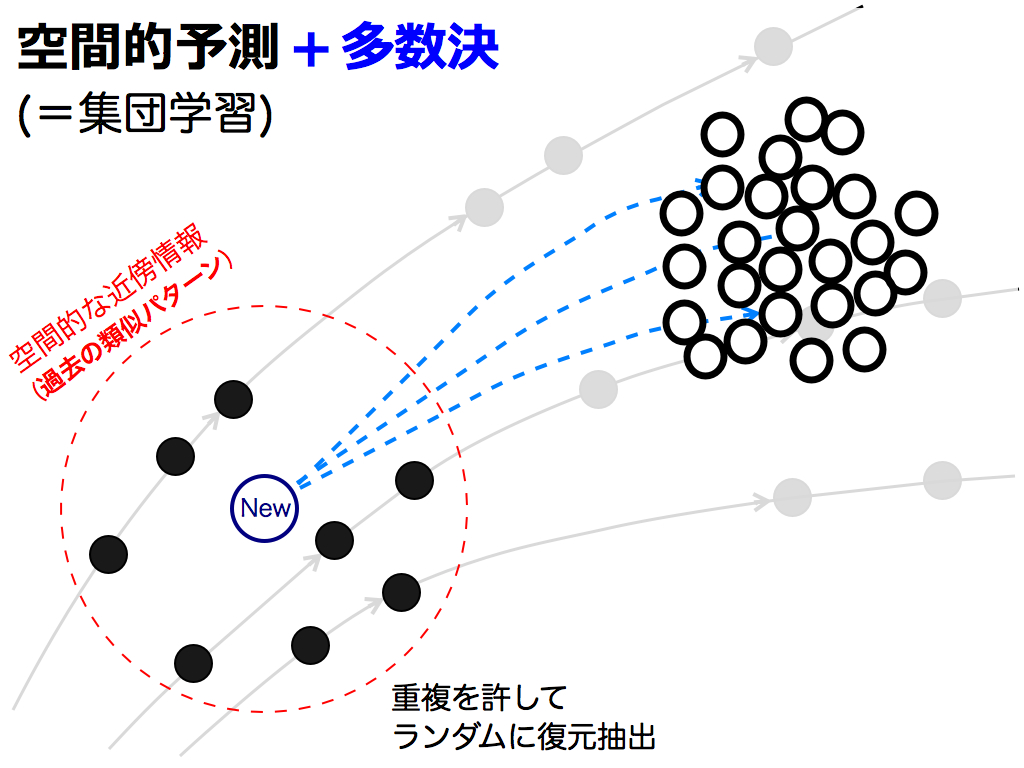
つまり,これらの予測値が「集団の意見」に相当します.例えば近傍点が8個ある場合,8^8=16777216通りの選び方ができます.しかし実際には,1000回程度繰返すことで,予測値の散らばり具合(=分布)を把握できます.
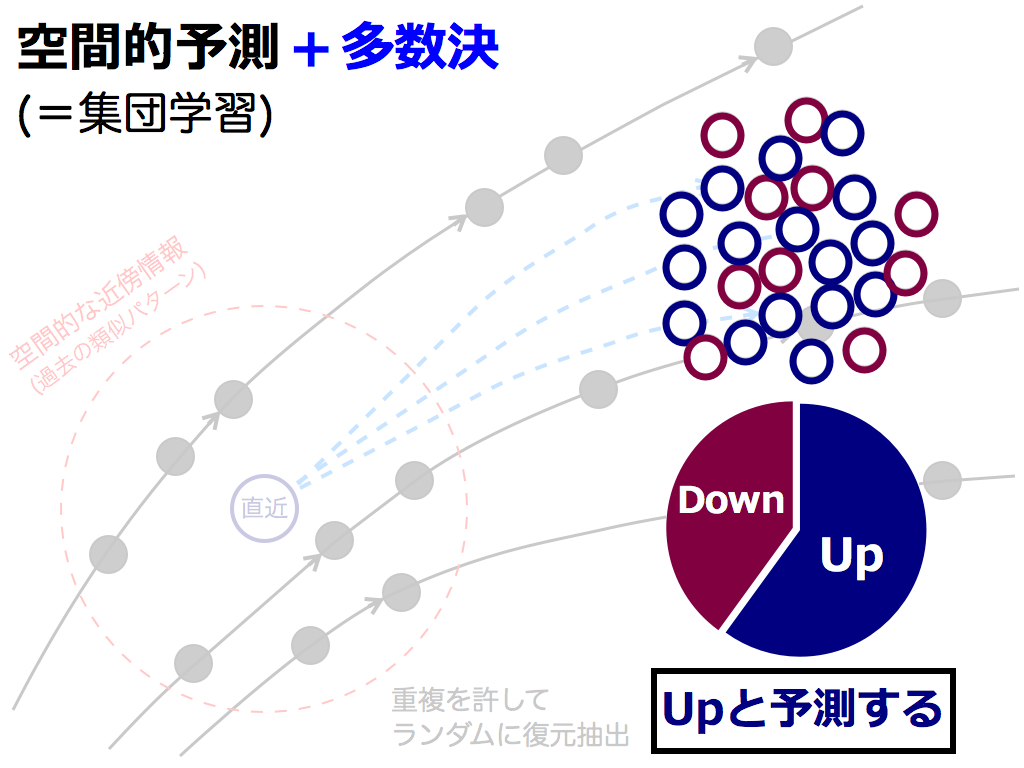
さて,多数決を取ってみましょう.もし,明日の株はUpすると言う予測値が,Downすると言う予測値より多い場合,「Up」を最終予測値とします.その逆の場合は「Down」を最終予測値とします.

この予測法を適用した実例を紹介します.東証一部上場企業200銘柄(日次データ)に対して,5年間予測した結果です. Up/Downの2択問題なので,勝率50%が基準です.結果として,7.4割の銘柄においてこの基準をクリアできています.しかし,勝率の平均値は高々54%です. やはり実際の金融市場の予測は簡単ではありません.
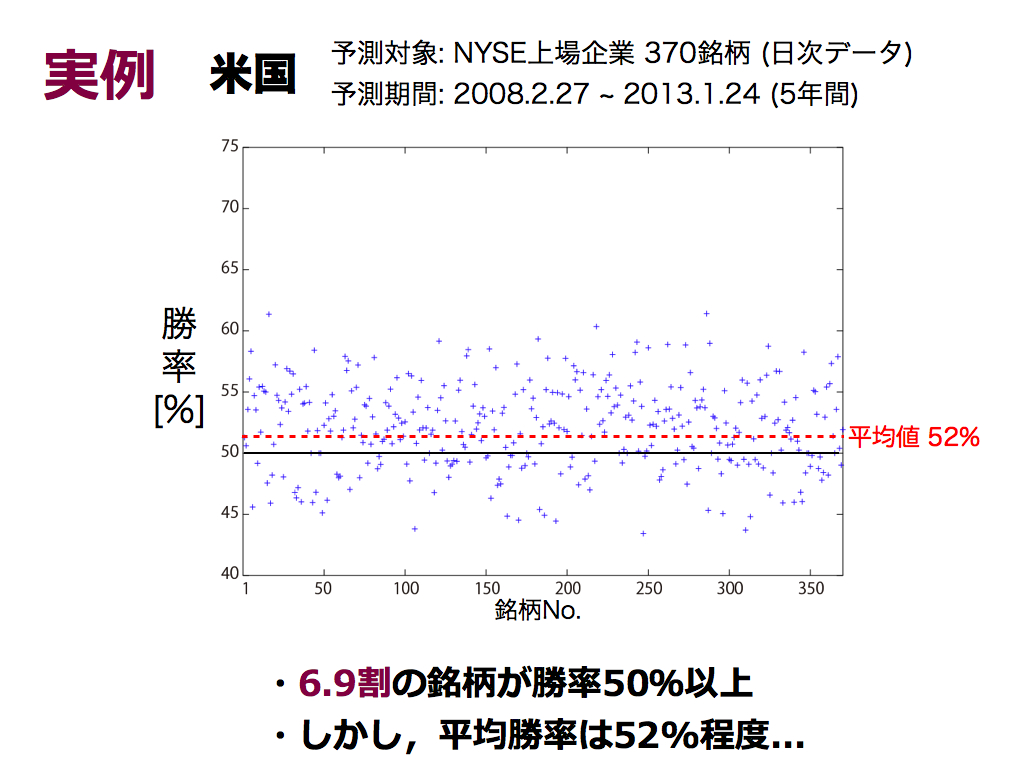
米国の実例です.NYSE上場企業の370銘柄(日次データ)に対して,5年間予測しました.日本の結果と同様に,約7割の銘柄において勝率50%以上を実現していますが, 勝率の平均値は高々52%で,十分に高くはありません.
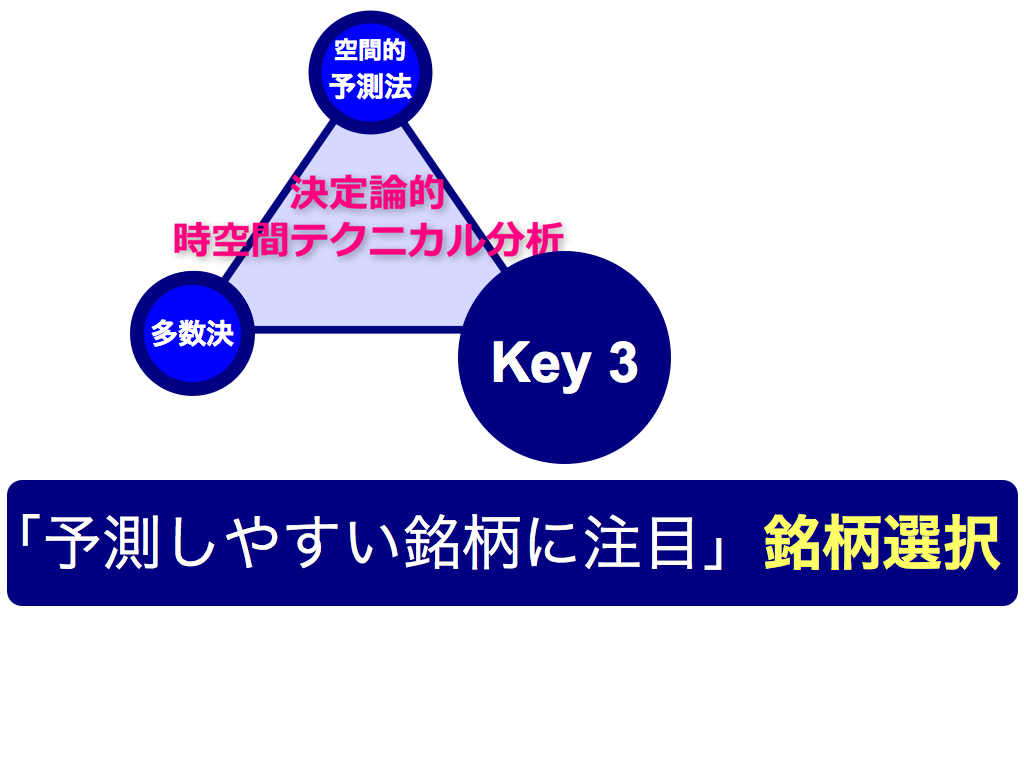
そこで第3のカギを紹介します.「銘柄選択」です. 予測しやすい銘柄に特化すれば良いのです.

これまでの予測法に基づいて,「多数決一致率」という新しいテクニカル指標を定義します.単に「Up意見の割合」を算出するだけです.
この指標の使い方も単純です.値が大きいほど集団の意見が一致し,Up予測に自信があるわけですから,基準値θを超えたらロングポジションを取ります.手仕舞い方法は色々考えられますが,今回は単純に翌日決済します.

基準値θは,バックテストで決定します.今回は,投資開始日以前の過去5年間において,投資成績(資産増加倍率)を最良にする基準値に設定しました.
この時の資産増加倍率を示します.いくつか投資成績が良い銘柄を確認できますので「銘柄選択」できそうです.しかしご注意ください.これはバックテスト(過去)の結果であり,未来の投資成績を保障しません.
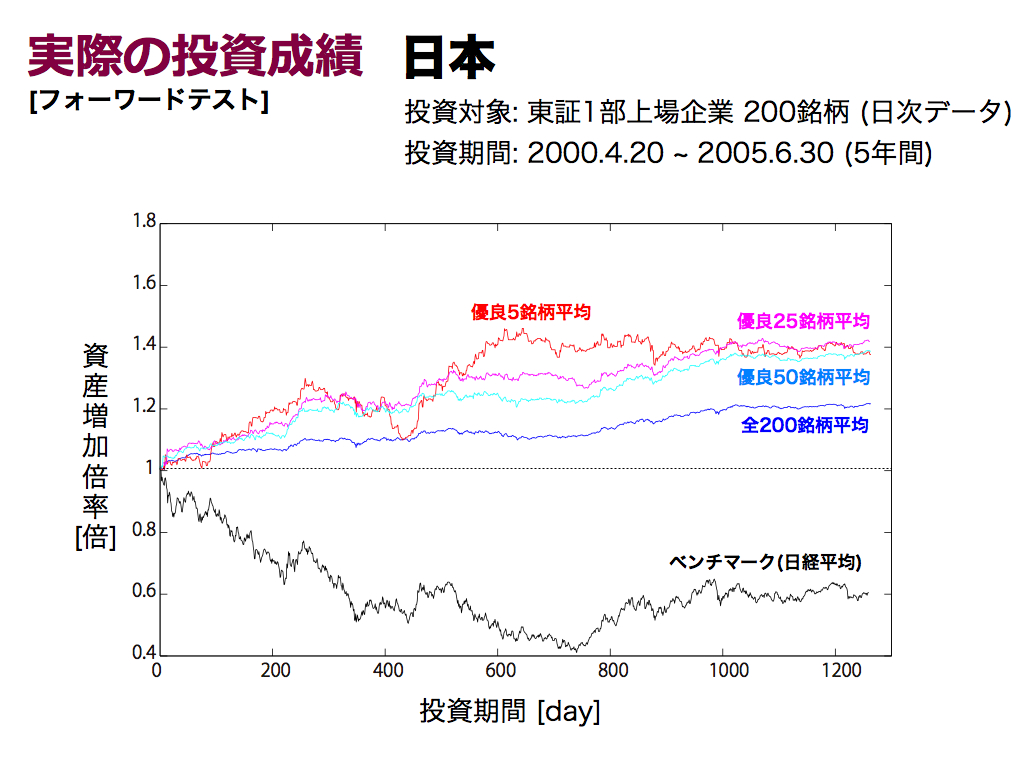
肝心なのはフォーワードテスト(未来)の結果です.そこで基準値θをバックテストによる最良値に固定して,以後5年間の投資を行いました.
スライドは日本市場の結果です.ベンチマーク(日経平均)よりも,優れた投資成績を実現できています.全200銘柄平均(銘柄選択なし)では,高々1.2倍の資産増加ですが,前スライドのように銘柄厳選することで,投資成績を向上できています.
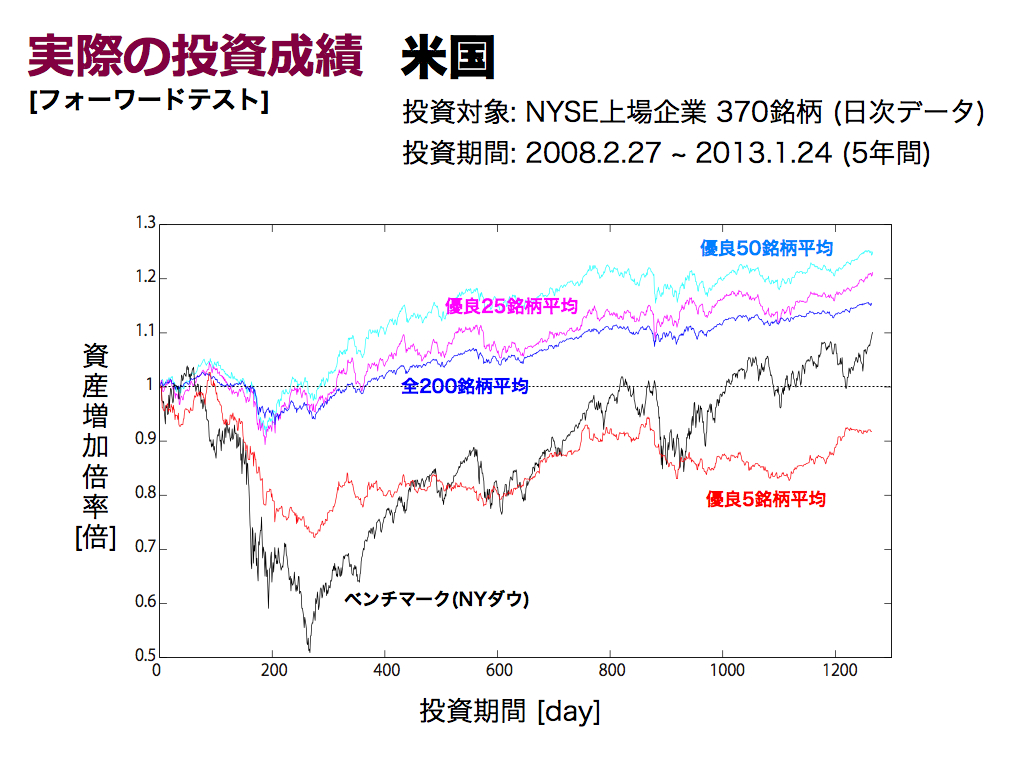
同様に,米国市場の結果です.全200銘柄平均(銘柄選択なし)は,ベンチマーク(NYダウ)より優秀です.また銘柄厳選として,優良銘柄に絞る効果も確認できます. しかし最良5銘柄平均では成績が悪化しています.つまり5銘柄では欲張りすぎと言えます.これはバックテストに基づく銘柄厳選ですから,必ずしもフォーワードテストに当てはまるとは言えません. そこである程度の銘柄数が必要になります.しかし銘柄厳選が効いても,資産増加倍率は高々1.3程度であります.
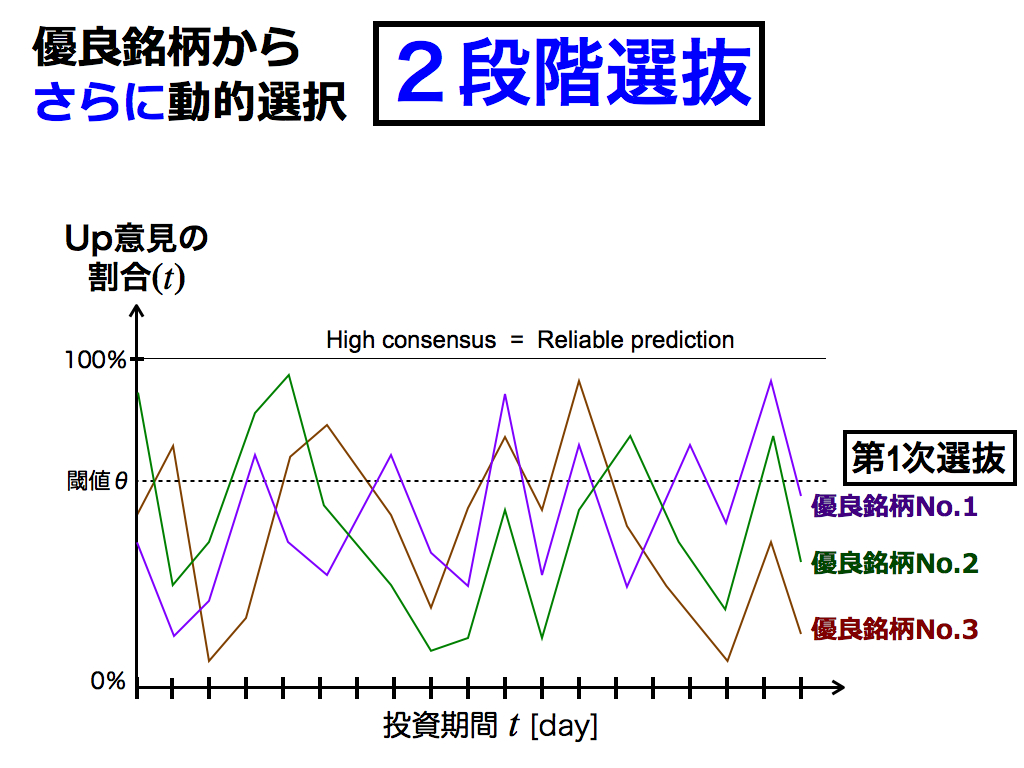
そこで,次の一手は「2段階選抜」です. このバックテストによる選抜を第1次選抜とし,ある程度優良な(予測しやすい)銘柄に目星をつけておきます.各銘柄のテクニカル指標は,スライドのように時変します.

第2次選抜では,フォーワードテスト中の各時刻において,多数決一致率が最大の銘柄を1つ選び,集中投資します. これは第1次選抜である程度予測可能と認められた銘柄の中で,尚かつ多数決のコンセンサス(予測への自信)が最大であるため,最も有望な銘柄と考えられます.

この結果を示します.第1次選抜での銘柄数(5または25)で投資成績は異なりますが,いずれにせよ2段階選抜によって,投資成績を飛躍的に向上できています.
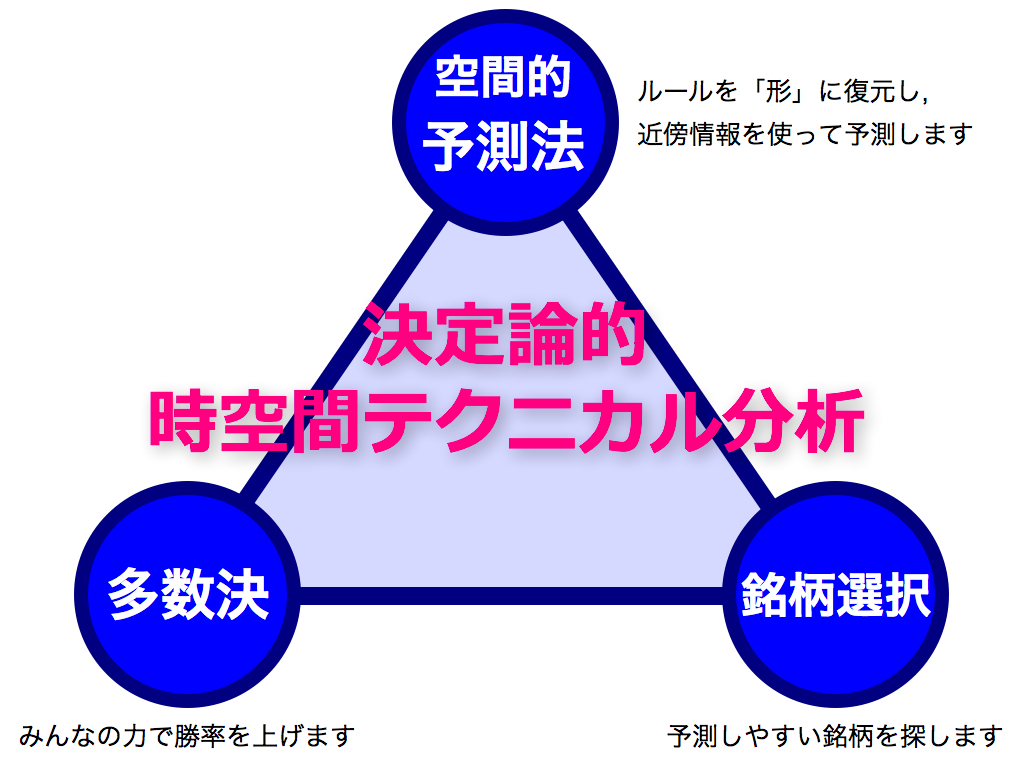
以上で「3つのカギ」が揃いました.
第1は「空間的予測法」です.これは,価格データを生み出すルールFを形として再現し,近傍点の動きを模倣することで将来予測を行います.非常にシンプルかつパワフルな予測法です.
第2は「多数決」です.工学では集団学習と呼ばれ,頼りない予測法でも複数寄せ集めることで予測力を向上できます.この理屈は確率統計に基づいて証明できます. 第3は「銘柄選択」です.バックテストにおいて予測しやすい銘柄を複数選出し,次にフォーワードテストの各時刻において,最も予測に自信のある銘柄に集中投資します.本稿のタイトル「決定論的時空間テクニカル分析」は,これら3つのコンセプトによって構成されます.
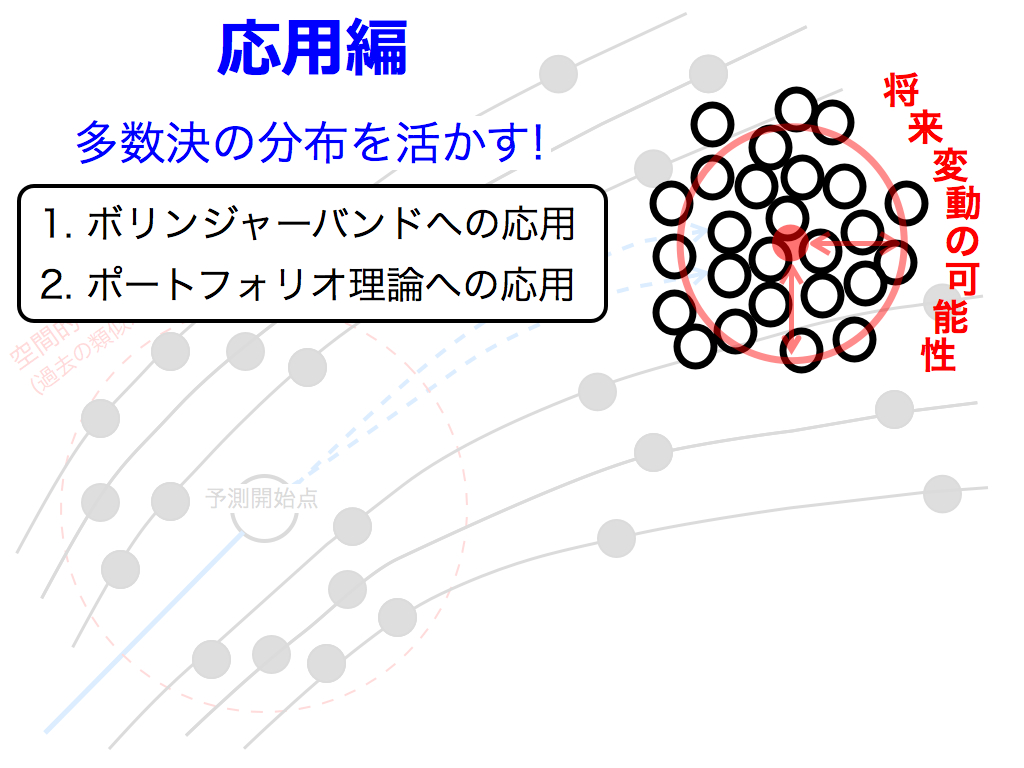
これより,応用編です.
集団学習による予測値の散らばりを,将来変動の可能性(確率分布)と捉えることで,本手法を「ボリンジャーバンド」や「ポートフォリオ理論」に応用します.
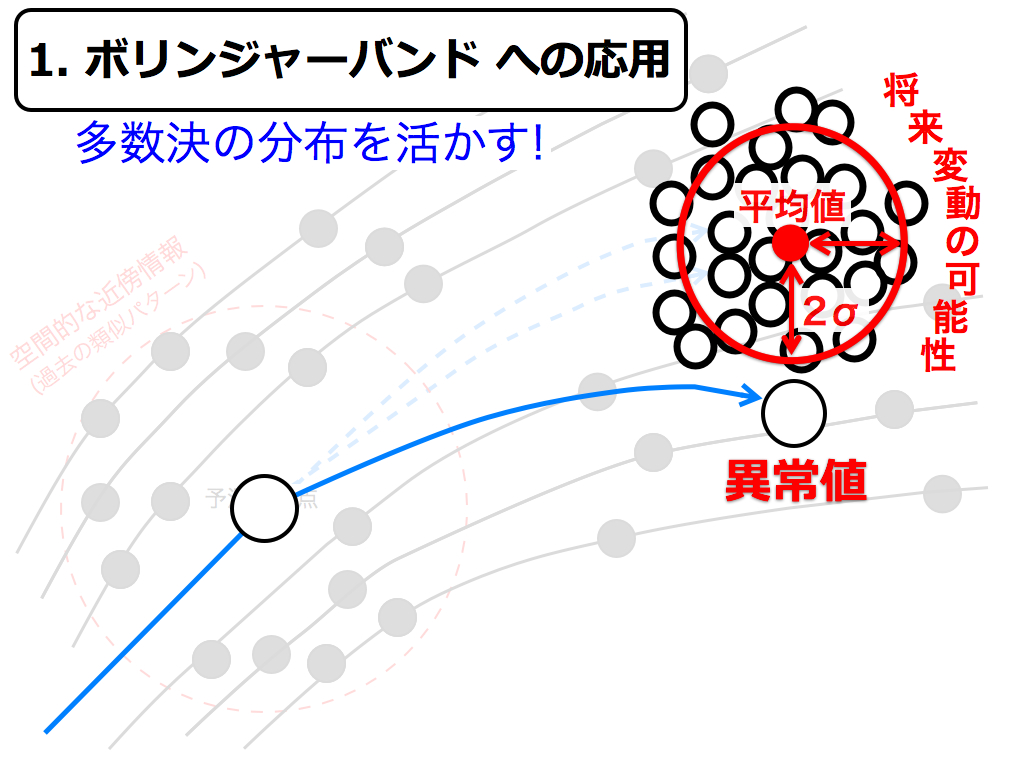
まずはボリンジャーバンドへ応用します.
多次元空間に変換した収益率変動が,確率分布の2シグマを超えたら,それは異常に大きな変動とみなせるでしょう. この考え方は,ボリンジャーバンドと同様に,統計学に基づいています.
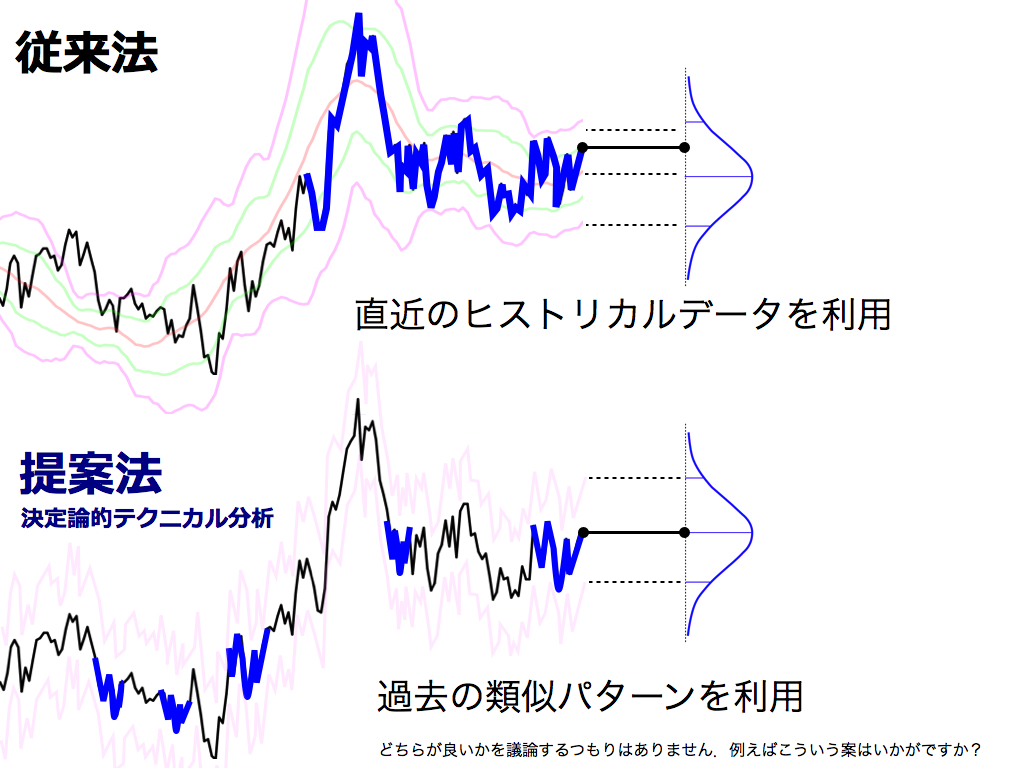
ところで,通常のボリンジャーバンド(従来法)と,決定論的テクニカル分析(提案法)の違いは何でしょうか.
従来法では直近のヒストリカルデータを収集して確率分布を構成します.一方,提案法では,過去の類似パターン(近傍点)に基づいて予測をし, 集団学習法によって予測値に多様性を持たせることで確率分布を構成します. つまり,確率分布の構築に用いるデータの根拠として,従来法では「時間的近さ」が重要であり,提案法では「空間的近さ」(変動パターンの類似性) を重要視しています.
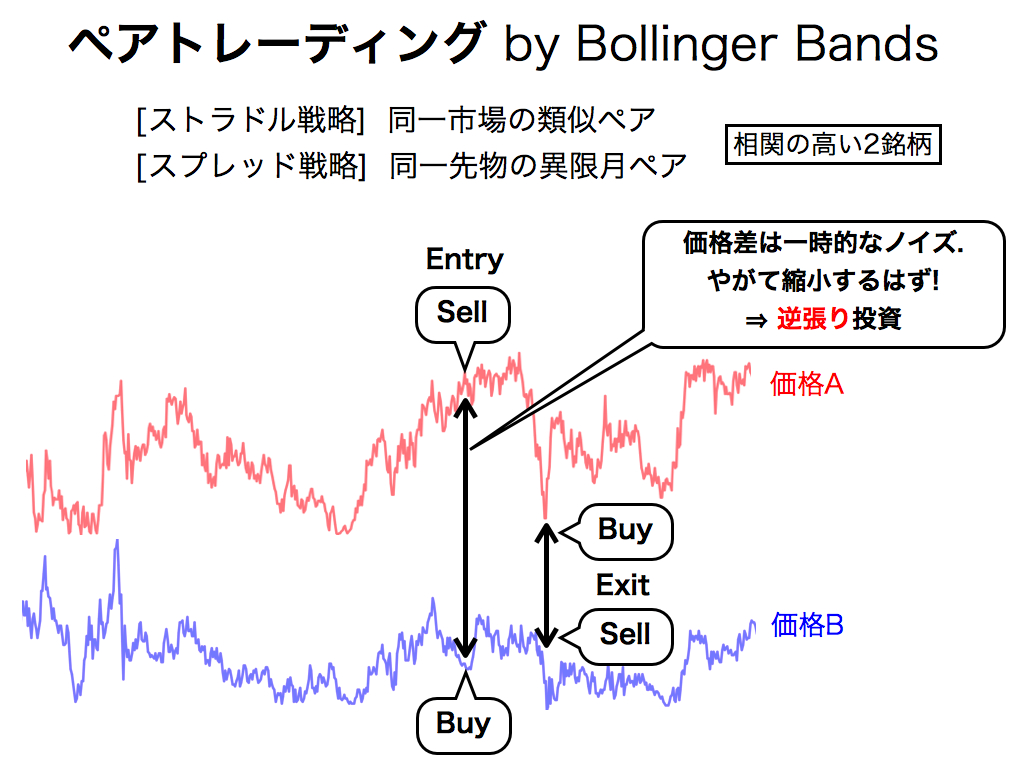
本稿では,ボリンジャーバンドを「ペアトレーディング」に活用してみます. ストラドル戦略やスプレッド戦略などありますが,いずれも銘柄間価格差の中心回帰性を狙った戦略です. つまり価格差が異常に拡大した時にエントリーし,価格差の縮小時に反対売買によっての収益を得る逆張り投資法です.
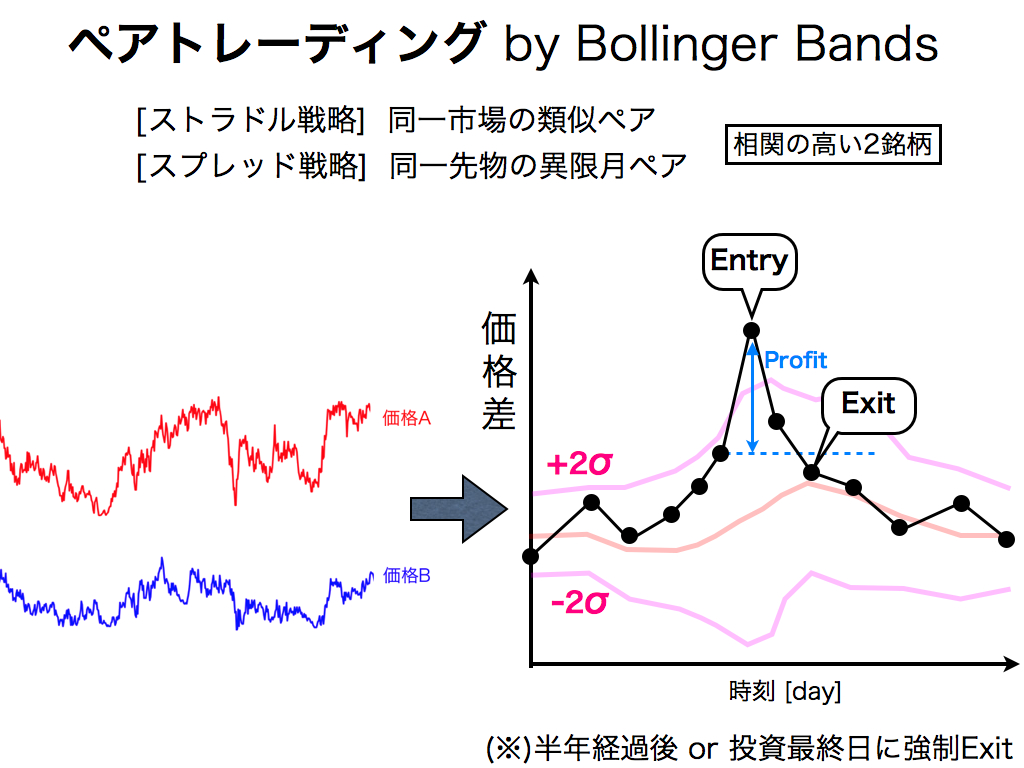
本稿では,銘柄間価格差が分布の2シグマを超えたらエントリーし,元の価格差以下に縮小したら決済します. なおリスク管理として,半年経過しても決済できない場合は強制的に手仕舞いします.また各限月の最終日や投資最終日でも強制的に手仕舞いします.

ストラドル戦略(米国株式)の投資成績です.NYSE上場企業1777ペア(日次データ)に対する,5年間の資産増加倍率(全ペアの平均値)です.
従来法もベンチマーク超えており優秀ですが,提案法の方が高成績を示しています.なおバックテストに基づいて1777ペアから上位10ペアに銘柄選択したところ,提案法において更なる投資成績の向上を確認できます.
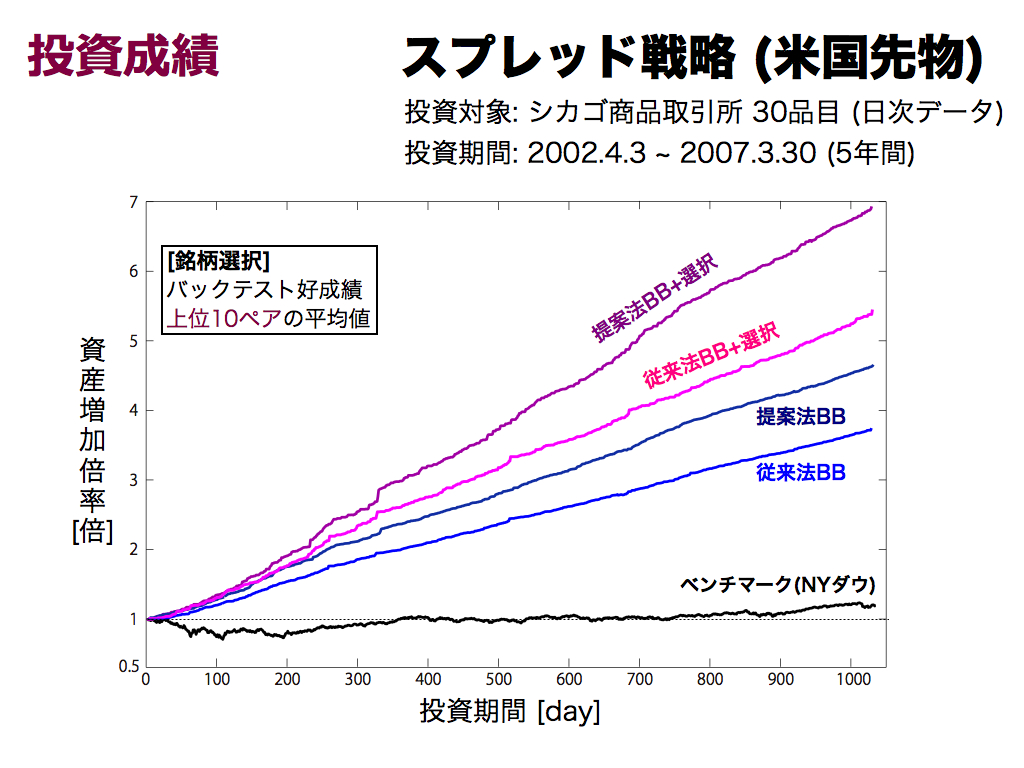
スプレッド戦略(米国先物)の投資成績です.シカゴ商品取引所上場30品目(日次データ)に対する,5年間の資産増加倍率(全ペアの平均値)です.
こちらも同様に,従来法の有用性および銘柄選択の有用性を確認できます.なお,従来法も良好です.
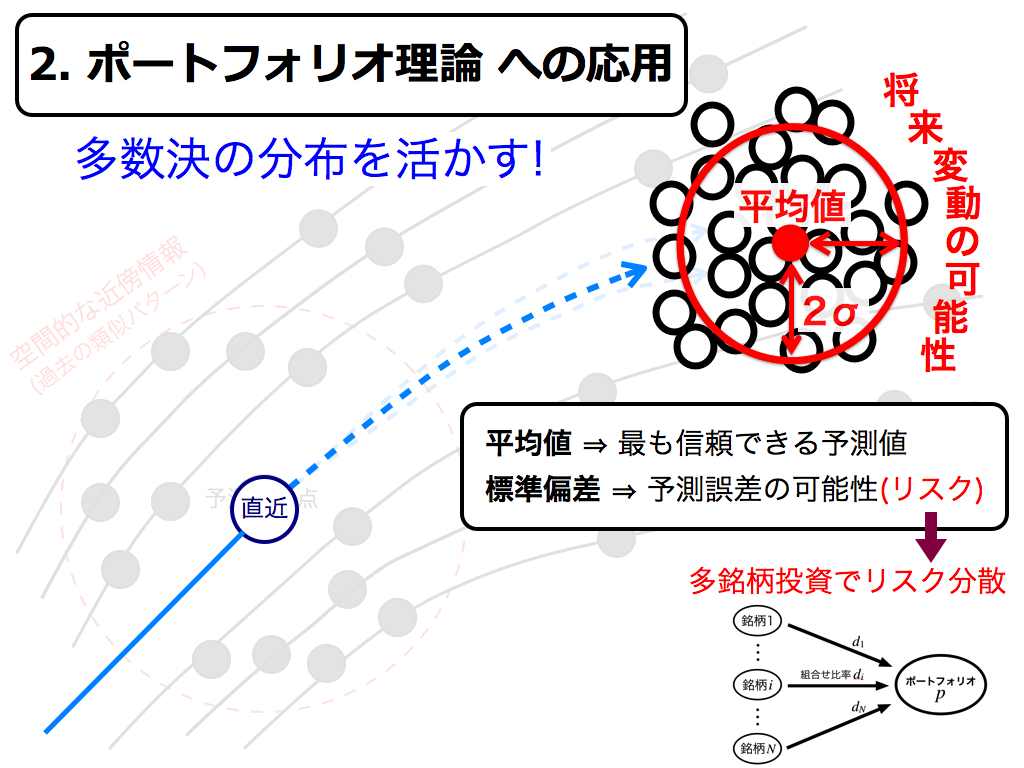
2つ目の応用事例として,ポートフォリオ理論をご紹介します.先と同様に,集団学習で得られた予測値の散らばりを,将来変動の可能性を表す確率分布と考えれば,この平均値(期待値)は,最も信頼できる予測値です. しかし,標準偏差に応じた予測誤差の危険性(リスク)も存在します.そこでこのリスクを低減すべく,分散投資を行います.
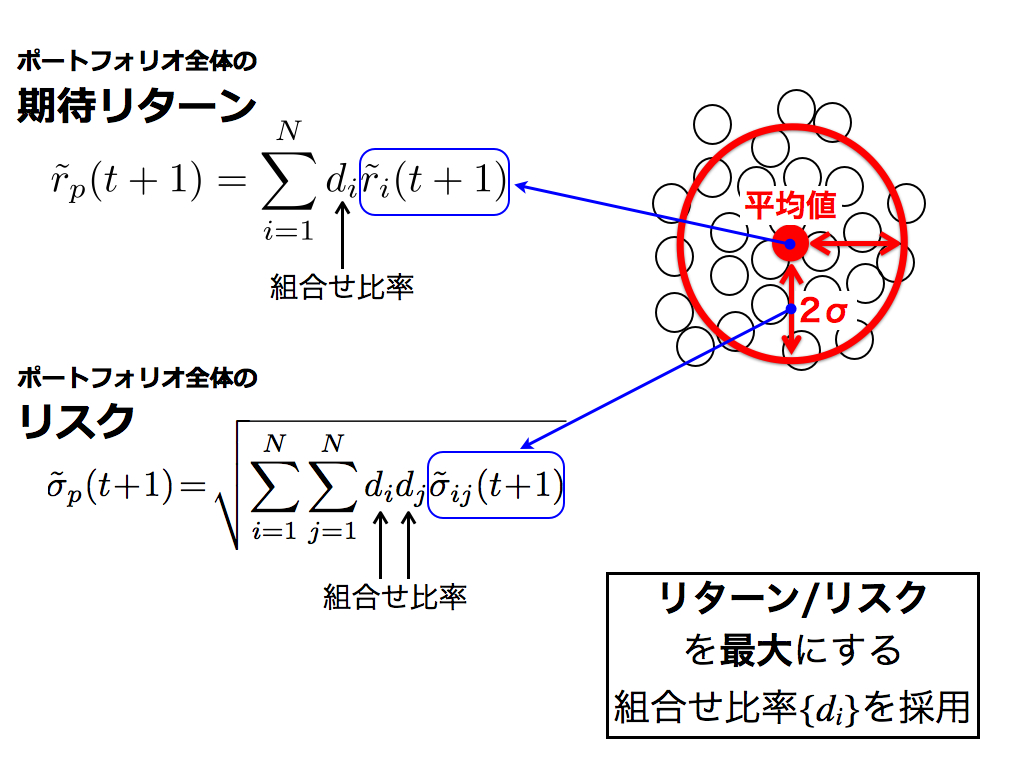
ご存知の通り,これらの数式はポートフォリオ理論(平均分散モデル)によるものです.添え字pはポートフォリオ全体を意味し,iは個別銘柄を意味します.
ポートフォリオを最適化するには,期待リターン/リスクを最大化する組合せ比率{di}を採用します.ここで,期待リターンは確率分布の平均値,リスクは標準偏差によって推定されます.
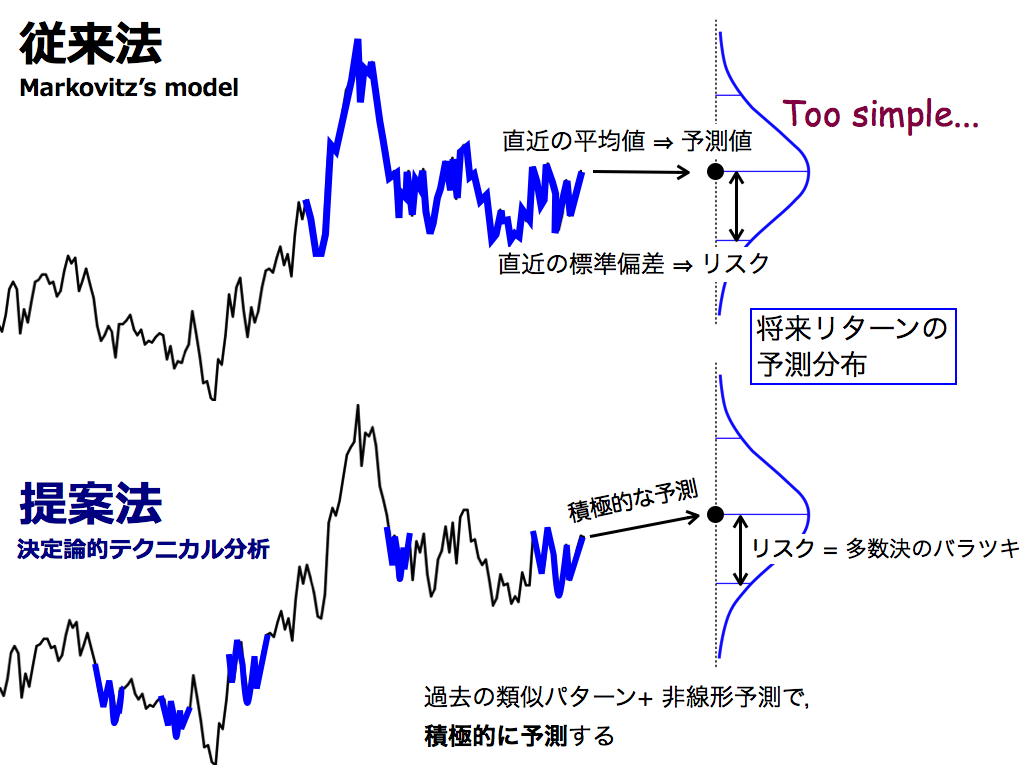
さて,従来法と提案法の違いは何でしょうか.ボリンジャーバンドと同様に,従来法では「時間的近さ」,提案法では「空間的近さ」(変動パターンの類似性) を重視します. また従来法では,直近の平均値(移動平均値)を将来の予測値とするため,予測法としては非常に単純です. しかし提案法では,過去の類似パターン(フォーメーション)を利用して積極的に予測するため,従来法の予測力を強化した方法と考えらえます.

次に,銘柄選択の可能性を検証すべく,バックテストと投資期間の予測精度の相関図を示します.投資開始時において前者は既知情報ですが,後者は未知情報です. しかし両者に相関があれば,バックテストの結果から未知である投資期間の予測精度を予想できるため,有望銘柄の選択が可能になります.
結果より,従来のポートフォリオモデルでは相関は低く,銘柄選択は難しいと言えます.そもそも移動平均による単純な予測であるため,予測精度が低いです.一方,提案法では,相関係数が高く,バックテストの予測精度に基づいて,優良銘柄の選択ができそうです.
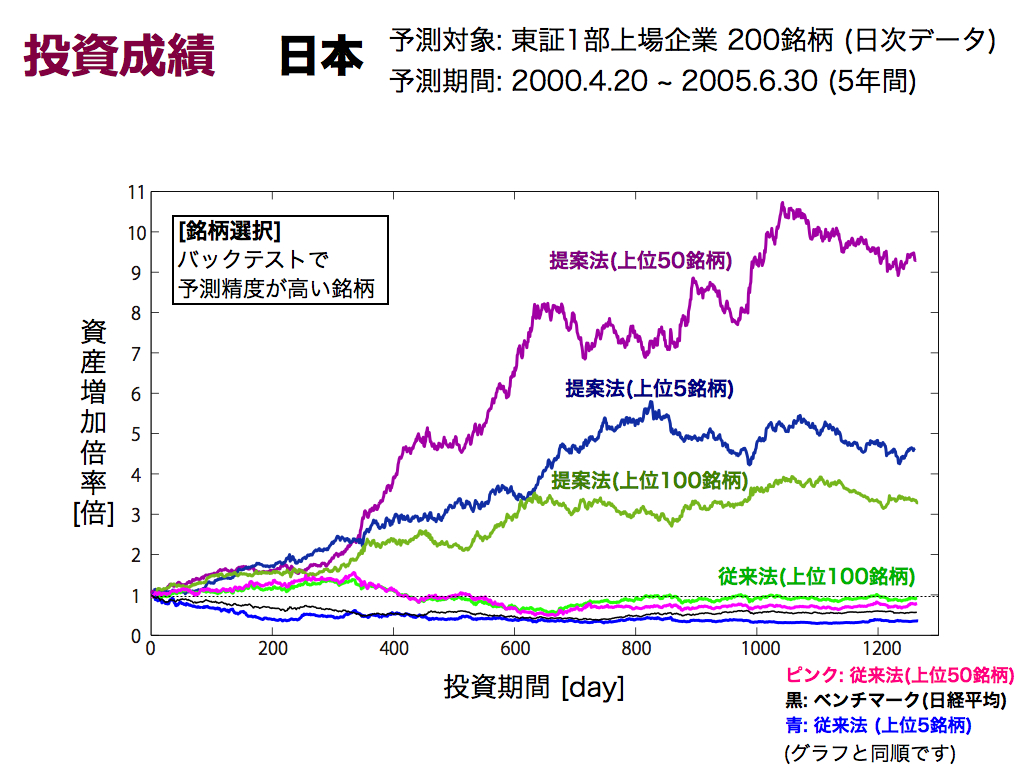
日本での投資成績を示します.東証上場企業200銘柄(日次データ)から有望な銘柄に厳選してポートフォリオを組み,5年間運用した結果です.
ベンチマークおよび従来法は1倍を下回っており,投資が難しい時期であると言えます.しかし提案法による投資成績は良好であり,バックテストによる銘柄選択も効果を発揮しています. しかし上位5銘柄による銘柄厳選は,欲張りすぎと考えられます.
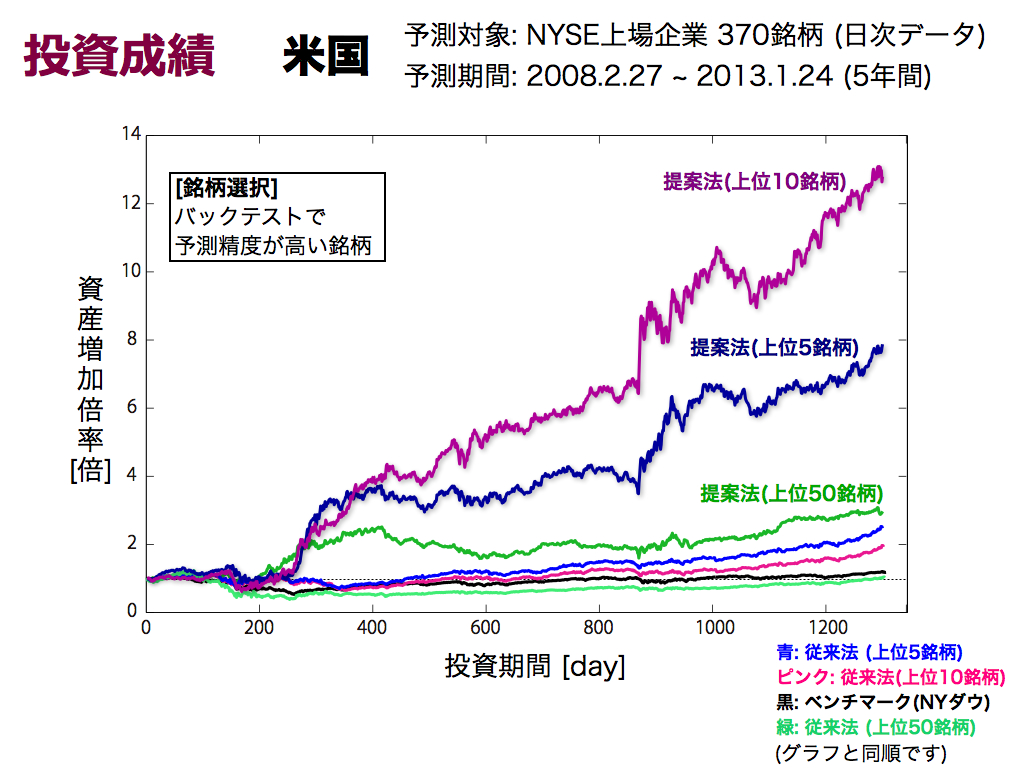
米国の結果です.NYSE上場企業370銘柄(日次データ)から有望な銘柄に厳選してポートフォリオを組み,5年間運用した結果です.
結果は日本と同様です.ベンチマークおよび従来法は1倍程度ですが,提案法および銘柄選択の有用性を確認でき,さらに欲張りすぎによる成績低下も確認できます.
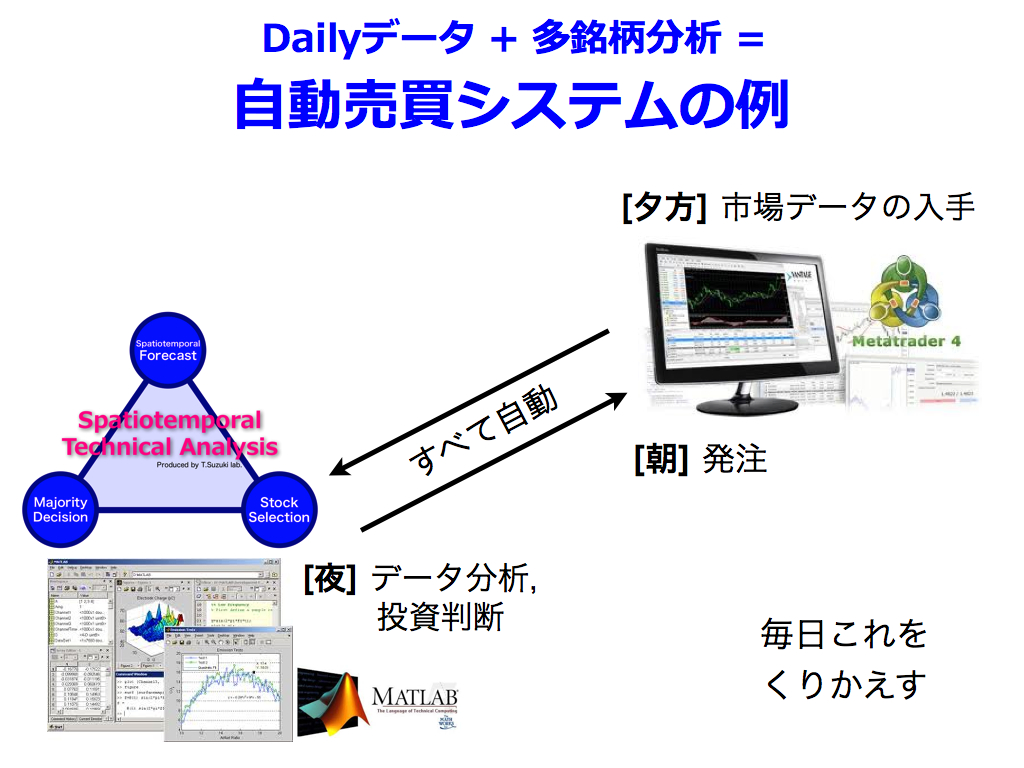
最後に「自動売買システム」をご紹介します.
本手法は,原則日次データを使用し,さらに有望銘柄を多くの銘柄から探索しますので,コンピュータの力を借ります. 最新データの取得はメタトレーダー(MT)が便利ですが,バージョンによって仕様が変わるので,あまり深入りしたくありません. そこで本稿の提案法(時空間テクニカル分析)においては,汎用のプログラミング環境であるMatlabで構築します. MTとMatlabにおいて常時フォルダー監視させることで,完全自動売買システムを構築することが可能です.

以上です.もしご質問やコメントがございましたら,メールでお寄せください.なお,本稿の英語版は こちら です.
[関連発表論文]
[1] T. Hayashi, T. Suzuki: “New Bollinger Bands for Nonlinear Technical Analysis of Pairs Trading,” Proc. of Nonlinear Theory and its Applications, pp.531-534, 2012.
[2] K. Tanaka, T. Suzuki: “Dynamical Portfolio Theory by Nonlinear Bagging Predictors,” Proc. of Nonlinear Theory and its Applications, pp.527-530, 2012.
[3] Y. Ohkura, T. Suzuki: “Nonlinear Technical Analysis Using Spatial Historical Data,” Proc. of Nonlinear Circuits, Communications and Signal Processing, pp.349-352, 2013.
[4] Y. Hirano, T. Hayashi,T. Suzuki: “Modified Bollinger Bands Based on Nonlinear Theory for Arbitrage Trading Strategies,” Proc. of Nonlinear Circuits, Communications and Signal Processing, pp.669-672, 2013.
[5] V. T. Thanh, S. Inose, T. Suzuki: “Automated Trading System Using the Nonlinear Portfolio Model Implemented by Matlab and MetaTrader,” Proc. of Nonlinear Circuits,Communications and Signal Processing, pp.229-232, 2014.
[6] 和知宏武, Vu Tat Thanh, 猪瀬悟史, 神成敦, 鈴木智也: “非線形ポートフォリオモデルを用いた外国為替自動取引システムの構築,” 電子情報通信学会信学技報, vol.113, no.383, NLP2013-132, pp.19-24, 2014.